

题目列表(包括答案和解析)
22、如图,在矩形ABCD中,AB=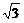 ,BC=a,又PA⊥平面ABCD,PA=4.
(1)若在边BC上存在一点Q,使PQ⊥QD,求a的取值范围;
(2)当BC上存在唯一点Q,使PQ⊥QD时,求异面直线AQ与PD所成角的大小;
(3)若a=4,且PQ⊥QD,求二面角A-PD-Q的大小.
,BC=a,又PA⊥平面ABCD,PA=4.
(1)若在边BC上存在一点Q,使PQ⊥QD,求a的取值范围;
(2)当BC上存在唯一点Q,使PQ⊥QD时,求异面直线AQ与PD所成角的大小;
(3)若a=4,且PQ⊥QD,求二面角A-PD-Q的大小.
解:
(1)、以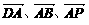 为x、y、z轴建立空间直角坐标系,则
为x、y、z轴建立空间直角坐标系,则
B(0,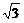 ,0),C(-a,
,0),C(-a,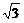 ,0),D(-a,0,0),P(0,0,4)
,0),D(-a,0,0),P(0,0,4)
设Q(t,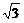 ,0),则
,0),则  =(t,
=(t,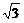 ,-4),
,-4),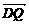 =(t+a,
=(t+a,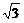 ,0)
∵PQ⊥QD,∴
,0)
∵PQ⊥QD,∴ =0 即t2+at+3=0 ①
∴△=a2-12≥0 Þ a≥2
=0 即t2+at+3=0 ①
∴△=a2-12≥0 Þ a≥2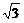 .
.
(2)、∵BC上存在唯一点Q,使PQ⊥QD,
∴△=a2-12=0 Þ a=2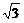 ,t=-
,t=-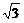
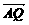 =(-
=(-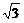 ,
,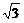 ,0) ,
,0) ,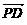 =(-2
=(-2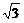 ,0,-4)
∴cos
,0,-4)
∴cos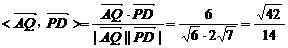 故异面直线AQ与PD所成角为arccos
故异面直线AQ与PD所成角为arccos .
.
(3)、过Q作QM∥CD交AD于M,则QM⊥AD,M(t,0,0) ∵PA⊥平面ABCD,∴PA⊥QM,又QM⊥AD,∴QM⊥平面PAD 过M作MN⊥PD于N,连结NQ,由三垂线定理知QN⊥PD ∴∠MNQ是二面角A-PD-Q的平面角
设N (m,0,n),则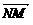 =(t-m,0,-n),
=(t-m,0,-n),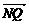 =(t-m,
=(t-m,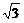 ,-n)
,-n)
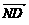 =(-4-m,0,-n) ∵MN⊥PD,ND、PD共线,∴
=(-4-m,0,-n) ∵MN⊥PD,ND、PD共线,∴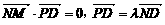
得:m+n-t=0,m-n=4 ② 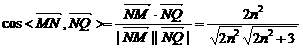
由①得:t=-1或t=-3,由②得:n=2+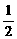 t
t
当t=-1时,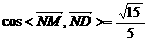 ,当t=-3时,
,当t=-3时,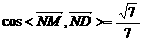
∴二面角A-PD-Q的大小为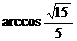 或
或 .
.
21、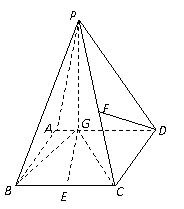 如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且PG=4,
如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且PG=4,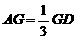 ,BG⊥GC,GB=GC=2,E是BC的中点.
,BG⊥GC,GB=GC=2,E是BC的中点.
(1)求异面直线GE与PC所成的角;
(2)求点D到平面PBG的距离;
(3)若F点是棱PC上一点,且DF⊥GC,求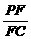 的值.
的值.
解:(1)解:以G点为原点,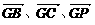 为x轴、y轴、z轴建立空间直角坐标系,
为x轴、y轴、z轴建立空间直角坐标系,
则B(2,0,0),C(0,2,0),P(0,0,4), 故E(1,1,0) 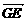 =(1,1,0),
=(1,1,0),
 =(0,2,4)
=(0,2,4) 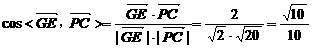
∴GE与PC所成的角为arccos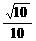 .
.
(2)解:平面PBG的单位法向量n=(0,±1,0) ∵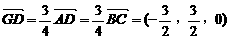
∴点D到平面PBG的距离为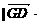 n |=
n |=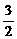
(3)解:设F(0,y,z),则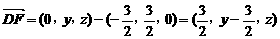
∵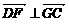 ,∴
,∴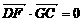 , 即
, 即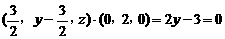 ,∴
,∴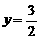 又
又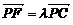 ,即(0,
,即(0,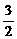 ,z-4)=λ(0,2,-4),∴z=1,
,z-4)=λ(0,2,-4),∴z=1,
故F(0,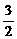 ,1)
,1) 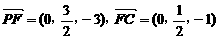 ,∴
,∴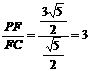
20、如图,已知点E是棱长为1的正方体 的棱
的棱 的中点,则点C到 平面
的中点,则点C到 平面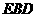 的距离等于
。
的距离等于
。
19、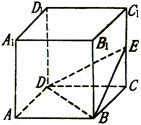 一个正方体的棱长为2,将八个直径各为1的球放进去之后,正中央空间能放下的最大的球的直径为
.
一个正方体的棱长为2,将八个直径各为1的球放进去之后,正中央空间能放下的最大的球的直径为
.
18、
17、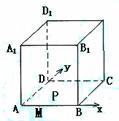 如图,正方体ABCD-A1B1C1D1的棱长为1,点M在棱AB上,且AM=
如图,正方体ABCD-A1B1C1D1的棱长为1,点M在棱AB上,且AM=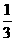 ,点P在平 面ABCD上,且动点P到直线A1D1的距离的平方与P到点M的距离的平方的差为1,在xAy直角坐标系中,动点P的轨迹方程是
.
,点P在平 面ABCD上,且动点P到直线A1D1的距离的平方与P到点M的距离的平方的差为1,在xAy直角坐标系中,动点P的轨迹方程是
.
16、在正三棱锥S-ABC中,侧棱SC⊥侧面SAB,侧棱SC= ,则此正三棱锥的外接球的表面积为
,则此正三棱锥的外接球的表面积为
15、半球内有一内接正方体, 正方体的一个面在半球的底面圆内. 若正方体的棱长为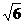 , 则半球
, 则半球
的体积为
14、长方体的长、宽、高分别为3cm、2cm、1cm,若该长方体的各顶点都在球O的表面上,则球O的表面积为
A.7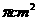 B.14
B.14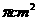 C.28
C.28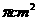 D.56
D.56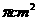
13、在下列命题中,真命题是
A. 直线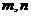 都平行于平面
都平行于平面 ,则
,则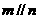
B.设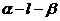 是直二面角,若直线
是直二面角,若直线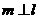 ,则
,则
C.若直线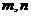 在平面
在平面 内的射影依次是一个点和一条直线,且
内的射影依次是一个点和一条直线,且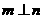 ,则
,则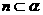 或
或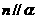
D.设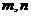 是异面直线,若
是异面直线,若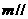 平面
平面 ,则
,则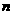 与
与 相交
相交
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com