
题目列表(包括答案和解析)
2.对卡方统计量的表达式的由来,学生只需要了解,作为探究问题可以在课后学习。
统计的基本思维模式是归纳的,它的特征之一是通过部分数据来推测全体数据的性质,因此,统计推断可能是错误的,也就是说,我们从数据上体现的只是统计上的关系,而不是因果关系
1.一般情况下,在尚未断定两个变量之间是否具有线性相关关系的情况下,应先进行相关性检验.在确认其具有线性相关关系后,再求其回归直线方程;由部分数据得到的回归直线,可以对两个变量间的线性相关关系进行估计,这实际上是将非确定性的相关关系问题转化成确定性的函数关系问题进行研究.由于回归直线将部分观测值所反映的规律性进行了延伸,它在情况预报、资料补充等方面有着广泛的应用。
题型1:线性相关性检验
例1.一个工厂在某年里每月产品的总成本y(万元)与该月产量x(万件)之间由如下一组数据:
|
x |
1.08 |
1.12 |
1.19 |
1.28 |
1.36 |
1.48 |
1.59 |
1.68 |
1.80 |
1.87 |
1.98 |
2.07 |
|
|
y |
2.25 |
2.37 |
2.40 |
2.55 |
2.64 |
2.75 |
2.92 |
3.03 |
3.14 |
3.26 |
3.36 |
3.50 |
|
1)画出散点图;2)检验相关系数r的显著性水平;3)求月总成本y与月产量x之间的回归直线方程.
解析:
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
xi |
1.08 |
1.12 |
1.19 |
1.28 |
1.36 |
1.48 |
1.59 |
1.68 |
1.80 |
1.87 |
1.98 |
2.07 |
|
yi |
2.25 |
2.37 |
2.40 |
2.55 |
2.64 |
2.75 |
2.92 |
3.03 |
3.14 |
3.26 |
3.36 |
3.50 |
|
xiyi |
2.43 |
2.264 |
2.856 |
3.264 |
3.590 |
4.07 |
4.643 |
5.090 |
5.652 |
6.096 |
6.653 |
7.245 |
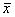 = = , , = = =2.8475, =2.8475, =29.808, =29.808, =99.2081, =99.2081, =54.243 =54.243 |
1)画出散点图:

2)
r=
=
在“相关系数检验的临界值表”查出与显著性水平0.05及自由度12-2=10相应的相关数临界值r0.05=0.576<0.997891, 这说明每月产品的总成本y(万元)与该月产量x(万件)之间存在线性相关关系
3)设回归直线方程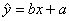 ,
,
利用
 ,
,
计算a,b,得b≈1.215,
a= ≈0.974,
≈0.974,
∴回归直线方程为: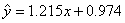

例2(2009泉州理)某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:

该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验
(Ⅰ)求选取的2组数据恰好是相邻两个月的概率;
 若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y关于x的线
若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y关于x的线
性回归方程 ;
;
(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认
为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
解
(1)设抽到相邻两个月的数据为事件A因为从6组数据中选取2组数据共有 中情况,每种情况都是等可能出现的其中,抽到相邻两个月的数据的情况有5种
中情况,每种情况都是等可能出现的其中,抽到相邻两个月的数据的情况有5种
所以
(Ⅱ)由数据求得
由公式求得
再由
所以y关于x的线性回归方程为
(Ⅲ)当 时,
时,
同样,当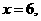 时,
时,
所以,该小组所得线性回归方程是理想的
题型2:独立性检验
例3.为了探究患慢性气管炎是否与吸烟有关,调查了339名50岁以上的人,调查结果如下表所示:
|
|
患慢性气管炎 |
未患慢性气管炎 |
合计 |
|
吸烟 |
43 |
162 |
205 |
|
不吸烟 |
13 |
121 |
134 |
|
合计 |
56 |
283 |
339 |
试问:50岁以上的人患慢性气管炎与吸烟习惯有关吗?
解析:由公式 ,因为7.469>6.635,所以我们有99%的把握说:50岁以上的人患慢性气管炎与吸烟习惯有关。
,因为7.469>6.635,所以我们有99%的把握说:50岁以上的人患慢性气管炎与吸烟习惯有关。
例4.(2009辽宁文)(本小题满分12分)某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品。从两个分厂生产的零件中个抽出500件,量其内径尺寸,的结果如下表:
甲厂
 试分别估计两个分厂生产的零件的优质品率;
试分别估计两个分厂生产的零件的优质品率;
(1)由于以上统计数据填下面 列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
|
|
甲 厂 |
乙 厂 |
合计 |
|
优质品 |
|
|
|
|
非优质品 |
|
|
|
|
合计 |
|
|
|
附: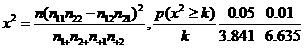


解 (1)甲厂抽查的产品中有360件优质品,从而甲厂生产的零件的优质品率估计为
 ;
;
乙厂抽查的产品中有320件优质品,从而乙厂生产的零件的优质品率估计为
(2)
|
|
甲厂 |
乙厂 |
合计 |
|
优质品 |
360 |
320 |
680 |
|
非优质品 |
140 |
180 |
320 |
|
合计 |
500 |
500 |
1000 |
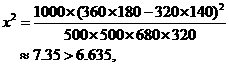


所以有99%的把握认为“两个分厂生产的零件的质量有差异”。
题型3:独立的概念及应用
例5.有三种产品,合格率分别是0.90,0.95和0.95,各抽取一件进行检验
(1)求恰有一件不合格的概率;
(2)求至少有两件不合格的概率(精确到0.001);
解析:设三种产品各抽取一件,抽到合格产品的事件分别为A、B和C,
(1)P(A)=0.90,P(B)=P(C)=0.95,则P( )=0.10,P(
)=0.10,P( )=P(
)=P( )=0.05。
)=0.05。
因为事件A、B、C相互独立,恰有一件不合格的概率为:
P(A·B· )+P(A·
)+P(A· ·C)+P(
·C)+P( ·B·C)
·B·C)
=P(A)·P(B)·P( )+P(A)·P(
)+P(A)·P( )·P(C)+P(
)·P(C)+P( )·P(B)·P(C)
)·P(B)·P(C)
=2×0.90×0.95×0.05+0.10×0.95×0.95≈0.176
答:恰有一件不合格的概率为0.176.
(2)解法一:至少有两件不合格的概率为:
P(A· ·
· )+P(
)+P( ·B·
·B· )+P(
)+P( ·
· ·C)+P(
·C)+P( ·
· ·
· )
)
=0.90×0.05×0.05+2×0.10×0.05×0.95+0.10×0.05×0.05≈0.012.
答:至少有两件不合格的概率为0.012.
解法二:三件产品都合格的概率为:
P(A·B·C)=P(A)·P(B)·P(C)=0.90×0.95×0.95≈0.812.
由(1)知,恰有一件不合格的概率为0.176,所以,至少有两件不合格的概率为1-[P(A·B·C)+0.176]=1-(0.812+0.176)=0.012.
答:至少有两件不合格的概率为0.012.
点评:本题主要考查互斥事件有一个发生的概率和相互独立事件概率的计算及运用数学知识解决问题的能力
例6.(2009山东卷理)某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的 

产品净重(单位:克)数据绘制的频率分布直方图,其中产品
净重的范围是[96,106],样本数据分组为[96,98),[98,100),
[100,102),[102,104),[104,106],已知样本中产品净重小于
100克的个数是36,则样本中净重大于或等于98克并且
小于104克的产品的个数是 ( ).
A.90 B.75 C. 60 D.45
答案 A
解析 产品净重小于100克的概率为(0.050+0.100)×2=0.300,
已知样本中产品净重小于100克的个数是36,设样本容量为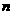 ,
,
则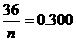 ,所以
,所以 ,净重大于或等于98克并且小于
,净重大于或等于98克并且小于
104克的产品的概率为(0.100+0.150+0.125)×2=0.75,所以样本
中净重大于或等于98克并且小于104克的产品的个数是
120×0.75=90.故选A.
[命题立意]:本题考查了统计与概率的知识,读懂频率分布直方图,会计算概率以及样本中有关的数据.
题型4:随机变量的分布列
例7.(2009全国卷Ⅱ理)(本小题满分12分)某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人,现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3名工人进行技术考核
(1)求从甲、乙两组各抽取的人数;
(I2)求从甲组抽取的工人中恰有1名女工人的概率;
(3)记 表示抽取的3名工人中男工人数,求
表示抽取的3名工人中男工人数,求 的分布列及数学期望。
的分布列及数学期望。


分析 (1)这一问较简单,关键是把握题意,理解分层抽样的原理即可。另外要注意
此分层抽样与性别无关。
(2)在第一问的基础上,这一问处理起来也并不困难。
从甲组抽取的工人中恰有1名女工人的概率
(3) 的可能取值为0,1,2,3
的可能取值为0,1,2,3
 ,
, ,
,
 ,
,
分布列及期望略.
评析:本题较常规,比08年的概率统计题要容易。在计算 时,采用分类的方
时,采用分类的方
法,用直接法也可,但较繁琐,考生应增强灵活变通的能力。
例8.设自动生产线在调整后出现废品的概率为0.1,而且一旦出现废品就要重新调整,求在两次调整之间所生产的合格品的数目不小于5的概率。
分析:如果用随机变量η表示两次调整之间生产的产品的个数,而且我们知道一旦出现废品就重新调整生产线,所以两次调整之间所生产的合格品是连续出现的,那么随机变量η的取值就服从几何分布,我们在解题时应先求出η的分布列。然后再计算事件“合格品数不小于5”即{η>5}的概率。
解析:设随机变量η表示两次调整之间生产线所生产的产品的个数,则η服从几何分布,事件{η=k}就表示生产了k-1件合格品,且第k件产品是废品。容易求得:
P(η=1)=0.1,
P(η=2)=(1-0.1)×0.1=0.09,
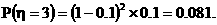
写成分布列的形式为:
 |
1 |
2 |
3 |
4 |
5 |
6 |
… |
|
P |
0.1 |
0.09 |
0.81 |
0.0729 |
0.06561 |
0.059049 |
… |
题目中要求计算“所生产的合格品数不小于5”的概率,即P(η>5),因为事件{η>5}所包含的基本事件为{η=6},{η=7},…,{η=n},…,所以有
P(η>5)=P(η=6)+P(η=7)+…+P(η=n)+…
我们应用分布列的性质计算上式的值.因为P(η>5)=1-P(η≤5),所以
P(η>5)=1-[P(η=1)+P(η=2)+P(η=3)+P(η=4)+P(η=5)]
=1-(0.1+0.09+0.081+0.0729+0.06561)=0.49049,
所以事件“两次调整之间所生产的合格品数不小于5”的概率为0.49049
点评:这是一道综合例题,包括了分列的计算及分布列的应用两个步骤。该题对于我们巩固所学知识,深入了解分布列有很大帮助
题型5:随机变量的均值
例9.(1)(2009湖南卷文) 一个总体分为A,B两层,用分层抽样方法从总体中抽取一个容量为
10的样本.已知B层中每个个体被抽到的概率都为 ,则总体中的个体数为 .
,则总体中的个体数为 .
答案 120
解析 设总体中的个体数为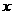 ,则
,则
(2)(2009四川卷文)设矩形的长为 ,宽为
,宽为 ,其比满足
,其比满足 ∶
∶ =
= ,这种矩形给人以美感,称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
,这种矩形给人以美感,称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
甲批次:0.598 0.625 0.628 0.595 0.639
乙批次:0.618 0.613 0.592 0.622 0.620
根据上述两个样本来估计两个批次的总体平均数,与标准值0.618比较,正确结论是
A.甲批次的总体平均数与标准值更接近
B.乙批次的总体平均数与标准值更接近
C.两个批次总体平均数与标准值接近程度相同
D.两个批次总体平均数与标准值接近程度不能确定
答案 A
解析 甲批次的平均数为0.617,乙批次的平均数为0.613
例10.设离散型随机变量 可能取的值为1,2,3,4。
可能取的值为1,2,3,4。 (
( 1,2,3,4)。又
1,2,3,4)。又 的数学期望
的数学期望 ,则
,则 ;
;
解析:设离散性随机变量 可能取的值为
可能取的值为 ,所以
,所以 ,即
,即 ,
,
又 的数学期望
的数学期望 ,则
,则 ,即
,即 ,
, ,∴
,∴ 
 。
。
点评:均值计算时要根据公式进行简化计算,从而达到简化运算的目的
题型6:随机变量的方差
例11.甲、乙两名工人加工同一种零件,两人每天加工的零件数相等,所得次品数分别为ε、η,ε和η的分布列如下:
|
ε |
0 |
1 |
2 |
η |
0 |
1 |
2 |
|
P |
 |
 |
 |
P |
 |
 |
 |
试对这两名工人的技术水平进行比较。
分析:一是要比较两名工人在加工零件数相等的条件下出次品数的平均值,即期望;二是要看出次品数的波动情况,即方差值的大小
解析:工人甲生产出次品数ε的期望和方差分别为:
 ,
,
 ;
;
工人乙生产出次品数η的期望和方差分别为:
 ,
,
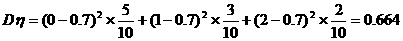 ;
;
由Eε=Eη知,两人出次品的平均数相同,技术水平相当,但Dε>Dη,可见乙的技术比较稳定。
点评:期望仅体现了随机变量取值的平均大小,但有时仅知道均值的大小还不够。如果两个随机变量的均值相等,还要看随机变量的取值如何在均值周围变化,即计算方差。方差大说明随机变量取值较分散,方差小说明取值分散性小或者取值比较集中、稳定。
题型7:正态分布
例12.2009全国卷Ⅱ文)(本小题满分12分)某车间甲组有10名工人,其中有4名女工人;
乙组有10名工人,其中有6名女工人。现采用分层抽样(层内采用不放回简单随即抽样)从甲、乙两组中共抽取4名工人进行技术考核
(1)求从甲、乙两组各抽取的人数;
(2)求从甲组抽取的工人中恰有1名女工人的概率;
(3)求抽取的4名工人中恰有2名男工人的概率。 

解析 本题考查概率统计知识,要求有正确理解分层抽样的方法及利用分类原理处理事件概率的能力,第一问直接利用分层统计原理即可得人数,第二问注意要用组合公式得出概率,第三问关键是理解清楚题意以及恰有2名男工人的具体含义,从而正确分类求概率.
解 (1)由于甲、乙两组各有10名工人,根据分层抽样原理,要从甲、乙两组中共抽
取4名工人进行技术考核,则从每组各抽取2名工人.
(2)记 表示事件:从甲组抽取的工人中恰有1名女工人,则
表示事件:从甲组抽取的工人中恰有1名女工人,则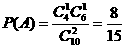


(3) 表示事件:从甲组抽取的2名工人中恰有
表示事件:从甲组抽取的2名工人中恰有 名男工人,
名男工人,
 表示事件:从乙组抽取的2名工人中恰有
表示事件:从乙组抽取的2名工人中恰有 名男工人,
名男工人,
 表示事件:抽取的4名工人中恰有2名男工人。
表示事件:抽取的4名工人中恰有2名男工人。


 与
与 独立,
独立, ,且
,且
故


6.正态分布
正态分布密度函数: ,均值为Eε=μ,方差为
,均值为Eε=μ,方差为 。
。
正态曲线具有以下性质:
(1)曲线在x轴的上方,与x轴不相交
(2)曲线关于直线x =μ对称
(3)曲线在x =μ时位于最高点。
(4)当x <μ时,曲线上升;当x >μ时,曲线下降。并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近。
(5)当μ一定时,曲线的形状由σ确定。σ越大,曲线越“矮胖”,表示总体越分散;σ越小,曲线越“瘦高”,表示总体的分布越集中。
从理论上讲,服从正态分布的随机变量 的取值范围是R,但实际上
的取值范围是R,但实际上 取区间(μ-3σ,μ+3σ)外的数值的可能性微乎其微,在实际问题中常常认为它是不会发生的。因此,往往认为它的取值是个有限区间,即区间(μ-3σ,μ+3σ),这即实用中的三倍标准差规则,也叫3σ规则。在企业管理中,经常应用这个规则进行产品质量检查和工艺生产过程控制。
取区间(μ-3σ,μ+3σ)外的数值的可能性微乎其微,在实际问题中常常认为它是不会发生的。因此,往往认为它的取值是个有限区间,即区间(μ-3σ,μ+3σ),这即实用中的三倍标准差规则,也叫3σ规则。在企业管理中,经常应用这个规则进行产品质量检查和工艺生产过程控制。
5.几种特殊的分布列
(1)两点分步
两点分布:对于一个随机试验,如果它的结果只有两种情况,则我们可用随机变量 ,来描述这个随机试验的结果。如果甲结果发生的概率为P,则乙结果发生的概率必定为1-P,所以两点分布的分布列为:
,来描述这个随机试验的结果。如果甲结果发生的概率为P,则乙结果发生的概率必定为1-P,所以两点分布的分布列为:
 |
1 |
0 |
|
P |
P |
1-p |
均值为E =p,方差为D
=p,方差为D =p(1-p)。
=p(1-p)。
(2)超几何分布
重复进行独立试验,每次试验只有成功、失败两种可能,如果每次试验成功的概率为p,重复试验直到出现一次成功为止,则需要的试验次数是一个随机变量,用ξ表示,因此事件{ξ=n}表示“第n次试验成功且前n-1次试验均失败”。所以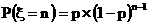 ,其分布列为:
,其分布列为:
|
ξ |
1 |
2 |
… |
n |
… |
|
P |
p |
p(1-p) |
… |
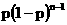 |
… |
(3)二项分布
如果我们设在每次试验中成功的概率都为P,则在n次重复试验中,试验成功的次数是一个随机变量,用ξ来表示,则ξ服从二项分布.则在n次试验中恰好成功k次的概率为:
二项分布的分布列为:
|
ξ |
0 |
1 |
… |
|
… |
n |
|
P |
 |
 |
… |
 |
… |
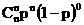 |
记ε是n次独立重复试验某事件发生的次数,则ε-B(n,p);其概率 …
… 。期望Eε=np,方差Dε=npq。
。期望Eε=np,方差Dε=npq。
4.随机变量的均值和方差
(1)随机变量的均值
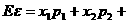 …;反映随机变量取值的平均水平
…;反映随机变量取值的平均水平
(2)离散型随机变量的方差:
 …
… …;反映随机变量取值的稳定与波动,集中与离散的程度。
…;反映随机变量取值的稳定与波动,集中与离散的程度。
基本性质: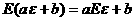 ;
; 。
。
3.独立
相互独立事件:事件A(或B)是否发生对事件B(或A)发生的概率没有影响.这样的两个事件叫做相互独立事件。
独立重复试验:若n次重复试验中,每次试验结果的概率都不依赖于其他各次试验的结果,则称这n次试验是独立的
公式
(1)两个相互独立事件同时发生的概率,等于每个事件发生的概率的积,即P(A·B)=P(A)·P(B);
推广:若事件A1,A2,…,An相互独立,则P(A1·A2…An)=P(A1)·P(A2)·…·P(n)。
(2)如果在一次试验中某事件发生的概率为P,那么在n次独立重复试验中这个事件恰好发生k次的概率:Pn(k)=C Pk(1-P)n-k。
Pk(1-P)n-k。
2.离散性随机变量的分布列
一般地,设离散型随机变量 可能取得值为:
可能取得值为:
X1,X2,…,X3,…,
 取每一个值Xi(I=1,2,…)的概率为P(
取每一个值Xi(I=1,2,…)的概率为P( ,则称表
,则称表
 |
X1 |
X2 |
… |
xi |
… |
|
P |
P1 |
P2 |
… |
Pi |
… |
为随机变量 的概率分布,简称
的概率分布,简称 的分布列。
的分布列。
两条基本性质:① …);②P1+P2+…=1。
…);②P1+P2+…=1。
1.随机变量的概念
如果随机试验的结果可以用一个变量来表示,那么这样的变量叫做随机变量。随机变量常用希腊字母ξ、η等表示。
对于随机变量可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量。
注:随机变量ξ是关于试验结果的函数,即每一个试验结果对应着一个实数;随机变量ξ的线性组合η=aξ+b(a、b是常数)也是随机变量。
2.卡方检验
统计中有一个有用的(读做“卡方”)统计量,它的表达式是:
 ,经过对统计量分布的研究,已经得到了两个临界值:3.841与6.635。当根据具体的数据算出的k>3.841时,有95%的把握说事件A与B有关;当k>6.635时,有99%的把握说事件A与B有关;当k
,经过对统计量分布的研究,已经得到了两个临界值:3.841与6.635。当根据具体的数据算出的k>3.841时,有95%的把握说事件A与B有关;当k>6.635时,有99%的把握说事件A与B有关;当k 3.841时,认为事件A与B是无关的。
3.841时,认为事件A与B是无关的。
随机变量
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com