
题目列表(包括答案和解析)
1.全集U=R , A=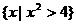 ,B={
,B={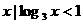 },
则A
},
则A (CuB)=( )
(CuB)=( )
A. {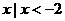 }
B. {
}
B. {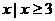 }
}
C. {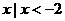 或
或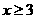 }
D. {
}
D. {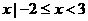 }
}
21.(本小题满分13分)
函数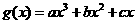 (
(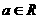 且
且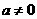 ),
),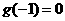 ,
,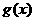 的导函数
的导函数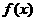 满足
满足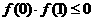 ,设
,设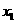 、
、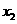 为方程
为方程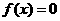 的两根。
的两根。
(1)求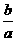 的取值范围;
的取值范围;
(2)若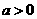 ,且当
,且当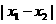 最小时,
最小时,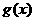 的极大值比极小值大
的极大值比极小值大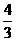 ,求
,求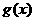 的解析式.
的解析式.
炎德·英才大联考高三月考试卷(八)
20.(本小题满分13分)
已知点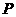 在椭圆
在椭圆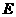 :
: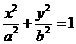
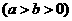 上,
上,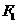 、
、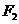 分别为椭圆
分别为椭圆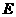 的左、右焦点,满足
的左、右焦点,满足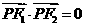 ,
,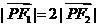 .
.
(1)求椭圆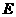 的离心率;
的离心率;
(2)若椭圆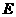 的长轴长为6,过点
的长轴长为6,过点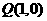 且不与
且不与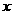 轴垂直的直线
轴垂直的直线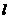 与椭圆
与椭圆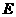 相交于两个不同点
相交于两个不同点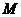 、
、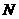 ,且
,且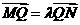 (
(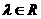 ,且
,且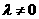 )。在
)。在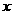 轴上是否存在定点
轴上是否存在定点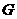 ,使得
,使得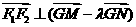 .若存在,求出所有满足这种条件的点
.若存在,求出所有满足这种条件的点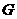 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
19.(本小题满分13分)
数列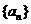 中,
中,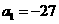 ,
,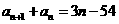 (
(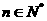 ).
).
(1)求证:数列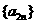 与
与 (
(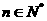 )都是等差数列;
)都是等差数列;
(2)若数列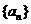 的前
的前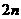 项和为
项和为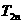 ,设
,设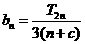 ,且数列
,且数列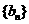 是等差数列,求非零常数
是等差数列,求非零常数 .
.
18.(本小题满分12分)
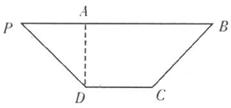
如图,在等腰梯形 中,
中,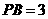 ,
,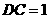 ,
,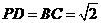 ,
, 为
为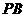 边上一点,且
边上一点,且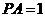 ,将
,将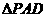 沿
沿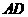 折起,使平面
折起,使平面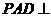 平面
平面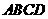 .
.
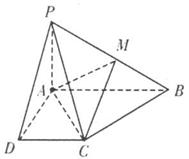
(1)求证:平面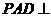 平面
平面 ;
;
(2)试在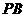 上找一点
上找一点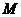 ,使截面
,使截面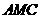 把几何体分成两部分,且
把几何体分成两部分,且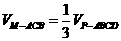 ;
;
(3)在(2)的条件下,判断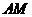 是否平行于平面
是否平行于平面 .
.
17.(本小题满分12分)
高三年级有7名同学分别获得校科技节某项比赛的一、二、三等奖,已知获一等奖的人数不少于1人,获二等奖的人数不少于2人,获三等奖的人数不少于3人.
(1)求恰有2人获一等奖的概率;
(2)求恰有3人获三等奖的概率.
16.(本小题满分12分)
已知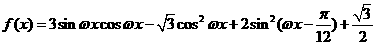 (其中
(其中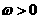 ).
).
(1)求函数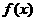 的值域;
的值域;
(2)若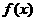 的周期为
的周期为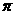 ,求
,求 的值并写出该函数在
的值并写出该函数在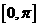 上的单调区间.
上的单调区间.
15.已知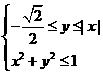 ,则点
,则点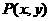 组成的图形面积为 .
组成的图形面积为 .
14.在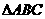 中,若
中,若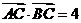 ,
,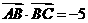 ,则
,则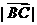 的值为
。
的值为
。
13.两位大学毕业生一起去一家单位应聘,面试前单位负责人对他们说:“我们要从面试的人中招聘3人,你们俩同时被招聘进来的概率是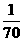 ”,根据这位负责人的话可以推断出参加面试的人数为 人.
”,根据这位负责人的话可以推断出参加面试的人数为 人.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com