
题目列表(包括答案和解析)
2.已知全集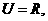 集合
集合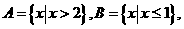 则
则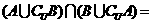
A.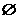 B.
B.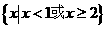 C.
C. 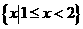 D.
D.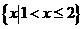
1.如果复数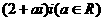 的实部与虚部互为相反数,则
的实部与虚部互为相反数,则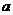 的值等于
的值等于
A.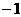 B.
B. C.
C.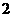 D.
D.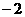
21.(本小题满分13分)已知直线L:x-y-3=0,抛物线C的顶点在原点,焦点在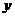 轴正半轴上,S是抛物线C上任意一点,T是直线L上任意一点,若|ST|的最小值为d>0时,点S的横坐标为2.
轴正半轴上,S是抛物线C上任意一点,T是直线L上任意一点,若|ST|的最小值为d>0时,点S的横坐标为2.
(1)求抛物线方程以及d的值;
(2)过抛物线C的对称轴上任一点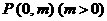 作直线与抛物线交于
作直线与抛物线交于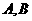 两点,点
两点,点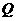 是点
是点 关于原点的对称点.设点
关于原点的对称点.设点 分有向线段
分有向线段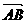 所成的比为
所成的比为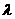 ,
,
证明: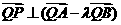 ;
;
(3)设R为抛物线准线上任意一点,过R作抛物线的两条切线,切点分别为M,N,直线MN是否恒过一定点?若恒过定点,请指出定点;若不恒过定点,请说明理由。
20.(本小题满分13分)若存在实常数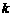 和
和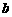 ,使得函数
,使得函数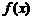 和
和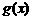 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: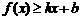 和
和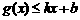 ,则称直线
,则称直线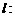
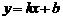 为
为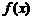 和
和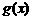 的“隔离直线”.已知
的“隔离直线”.已知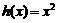 ,
,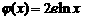 (其中
(其中 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求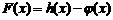 的极值;
的极值;
(Ⅱ) 函数 和
和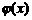 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
19. (本小题满分13分)货币是有时间价值的,现在的100元比一年后的100元价值要大些。例如银行存款的年利率为5%,那么现在的100元一年后就变为100(1+5%)=105元,而一年后的100元只相当于现在的 元,即一年后100元的现值为
元,即一年后100元的现值为 元。一般地,若银行的年利率为i,且在近n年内保持不变,则第n年后的a元的现值为
元。一般地,若银行的年利率为i,且在近n年内保持不变,则第n年后的a元的现值为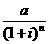 元。在经济决策时,常考虑货币的时间价值,把不同时期的货币化为其现值进行决策。某工厂年初欲购买某类型机器,有甲乙两种型号可供选择,有关资料如下:甲型机器购货款为10万元,每年年底支付的维护费用(维修、更换零件)第一年为1000元,第二年为2000元,……(以后每年比上年增加1000元);乙型机器购货款为6万元,每年年底支付的维护费用(大修理等)均为10000元。
元。在经济决策时,常考虑货币的时间价值,把不同时期的货币化为其现值进行决策。某工厂年初欲购买某类型机器,有甲乙两种型号可供选择,有关资料如下:甲型机器购货款为10万元,每年年底支付的维护费用(维修、更换零件)第一年为1000元,第二年为2000元,……(以后每年比上年增加1000元);乙型机器购货款为6万元,每年年底支付的维护费用(大修理等)均为10000元。
(1)若银行利率为i,分别求购买甲乙型机器使用n年总成本(购货款与各年维护费用之和)的现值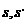 ,并求
,并求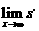
(2)若i=5%,两种型号机器均使用10年后就报废,请你决策选用哪种机器(总成本现值较小者)。(参考数据1.05-9=0.6446,1.05-10=0.6139,1.05-11=0.5874)
18.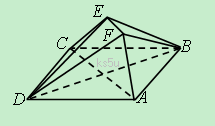 (本小题满分12分)如图,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EF//AC,∠CAF=∠AFE=90º,AB=
(本小题满分12分)如图,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EF//AC,∠CAF=∠AFE=90º,AB=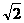 ,AF=FE=1.
,AF=FE=1.
(1)求证EC//平面BDF;
(2)求二面角A-DF-B的大小;
(3)试在线段AC上确定一点P,使得PF与
BC所成的角是60°.
17.(本小题满分12分)我校文化体育艺术节的乒乓球决赛在甲乙两人中进行,比赛规则如下:比赛采用7局4胜制(先胜4局这获胜即比赛结束),在每一局比赛中,先得11分的一方为胜方;比赛没有平局,10平后,先连得2分的一方为胜方
(1)根据以往战况,每局比赛甲胜乙的概率为0.6,设比赛的场数为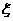 ,求
,求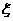 的分布列和期望;
的分布列和期望;
(2)若双方在每一分的争夺中甲胜的概率也为0.6,求决胜局中甲在以8:9落后的情况下最终以12:10获胜的概率。
16.(本小题满分12分)已知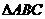 中,
中,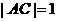 ,
,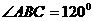 ,
, ,
,
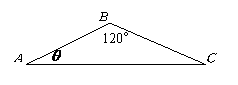 记
记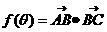 ,
,
(1)求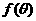 关于
关于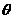 的表达式;
的表达式;
(2)求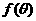 的值域;
的值域;
15.连掷两次骰子得到点数分别为m和n,记事件A为“所得点数m,n使得椭圆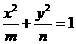 的焦点在x轴上”(1)P(A)= ;(2)若椭圆
的焦点在x轴上”(1)P(A)= ;(2)若椭圆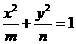 与椭圆
与椭圆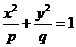 满足
满足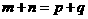 ,则称两椭圆为同和椭圆,从事件A所含的椭圆中随机抽取两个恰为同和椭圆的概率=
.
,则称两椭圆为同和椭圆,从事件A所含的椭圆中随机抽取两个恰为同和椭圆的概率=
.
14.若对于定义域任意x,总存在常数M,都有|f(x)|<M总成立,则称函数为有界函数。给定下列函数:①f(x)=2cos2x+sin2x,②g(x)= 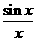 ,③h(x)=
,③h(x)= 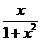 ,④p(x)=xe-x.其中有界函数的有
。(只填正确答案的序号)
,④p(x)=xe-x.其中有界函数的有
。(只填正确答案的序号)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com