
题目列表(包括答案和解析)
21.(本题12′)设函数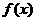 =-
=-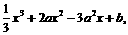 0<
0< <1。
<1。
(1)求函数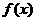 的单调区间、极值。
的单调区间、极值。
(2)若当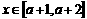 时,恒有
时,恒有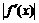 ≤
≤ ,试确定
,试确定 的取值范围。
的取值范围。
[解]:(1)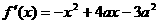 , 令
, 令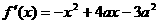 得x=a或x=3a
得x=a或x=3a
由表
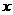 |
(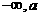 ) ) |
α |
(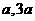 ) ) |
3α |
(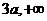 ) ) |
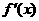 |
- |
0 |
+ |
0 |
- |
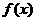 |
递减 |
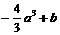 |
递增 |
b |
递减 |
可知:当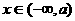 时,函数f (
时,函数f (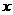 )为减函数,当
)为减函数,当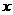
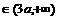 时,函数f(
时,函数f(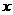 )也为减函数:当
)也为减函数:当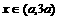 时,函数f(
时,函数f(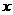 )为增函数。
)为增函数。
(2)由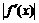 ≤
≤ ,得-
,得- ≤-
≤-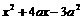 ≤
≤ 。∵0<
。∵0< <1, ∴
<1, ∴ +1>2
+1>2 ,
,
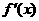 =-
=-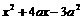 在[
在[ +1,
+1, +2]上为减函数。∴[
+2]上为减函数。∴[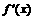 ]max =
]max =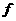 ′(
′( +1)=2
+1)=2 -1,
-1,
[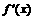 ]min=
]min=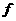 ′(
′( +2)=4
+2)=4 -4.于是,问题转化为求不等式组
-4.于是,问题转化为求不等式组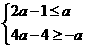 的解。
的解。
解不等式组,得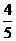 ≤
≤ ≤1。又0<
≤1。又0< <1, ∴所求
<1, ∴所求 的取值范围是
的取值范围是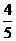 ≤
≤ ≤1。
≤1。
20、(本题12′)用长为18 cm的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
[解]:设长方体的宽为x(m),则长为2x(m),高为
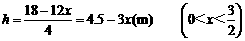 .
.
故长方体的体积为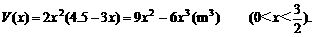
从而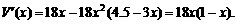
令V′(x)=0,解得x=0(舍去)或x=1,因此x=1.
当0<x<1时,V′(x)>0;当1<x<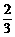 时,V′(x)<0,
时,V′(x)<0,
故在x=1处V(x)取得极大值,并且这个极大值就是V(x)的最大值。
从而最大体积V=V′(x)=9×12-6×13(m3),此时长方体的长为2 m,高为1.5 m.
答:当长方体的长为2 m时,宽为1 m,高为1.5 m时,体积最大,最大体积为3 m3。
19、(本题12′)在某次普通话测试中,为测试汉字发音水平,设置了10张卡片,每张卡片印有一个汉字的拼音,其中恰有3张卡片上的拼音带有后鼻音“g”,
(1)现对三位被测试者先后进行测试,第一位被测试者从这10张卡片总随机抽取1张,测试后放回,余下2位的测试,也按同样的方法进行。求这三位被测试者抽取的卡片上,拼音都带有后鼻音“g”的概率;
(2)若某位被测试者从10张卡片中一次随机抽取3张,求这三张卡片上,拼音带有后鼻音“g”的卡片不少于2张的概率.
[解]:(1)每次测试中,被测试者从10张卡片中随机抽取1张卡片上,拼音带有后鼻音“g”的概率为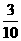 ,因为三位被测试者分别随机抽取一张卡片的事件是相互独立的,因而所求的概率为
,因为三位被测试者分别随机抽取一张卡片的事件是相互独立的,因而所求的概率为
(2)设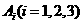 表示所抽取的三张卡片中,恰有
表示所抽取的三张卡片中,恰有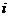 张卡片带有后鼻音“g”的事件,且其相应的概率为
张卡片带有后鼻音“g”的事件,且其相应的概率为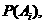 则
则
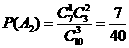 ,
, 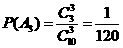
因而所求概率为 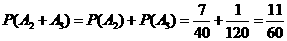
18、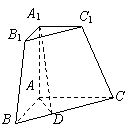 (本题12′)三棱锥被平行于底面
(本题12′)三棱锥被平行于底面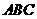 的平面所截得的几何体如图所示,截面为
的平面所截得的几何体如图所示,截面为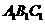 ,
,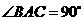 ,
, 平面
平面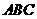 ,
, ,
, ,
, ,
, ,
,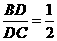 .
.
(1)证明:平面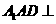 平面
平面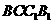 ;
;
(2)求二面角 的大小.
的大小.
解:(Ⅰ)如图,建立空间直角坐标系,
则 ,
,
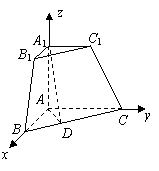
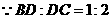 ,
,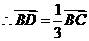 .
.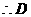 点坐标为
点坐标为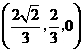 .
.

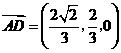 ,
,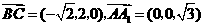 .
.
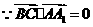 ,
,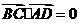 ,
,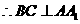 ,
,
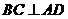 ,又
,又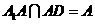 ,
,
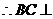 平面
平面 ,又
,又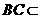 平面
平面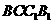 ,
, 平面
平面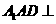 平面
平面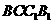 .
.
(Ⅱ)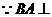 平面
平面 ,取
,取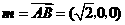 为平面
为平面 的法向量,
的法向量,
设平面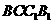 的法向量为
的法向量为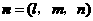 ,则
,则 .
.
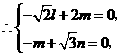
 ,如图,可取
,如图,可取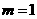 ,则
,则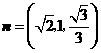 ,
,
 ,
,
即二面角 为
为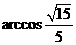 .
.
17.(本题10′)设函数 R),若使
R),若使 上为增函数,求a的取值范围.
上为增函数,求a的取值范围.
[解]: ,由题知:
,由题知:
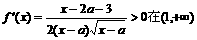 上恒成立
而
上恒成立
而
令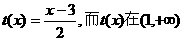 递增且最小值为
递增且最小值为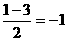 ,
,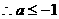
16.已知函数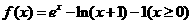 ,则函数f(x)的最小值是 0
,则函数f(x)的最小值是 0
15、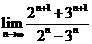 =
-3
=
-3
14、已知函数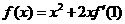 ,
, -2 .
-2 .
13.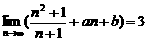 ,则
,则 3 。
3 。
12、设数列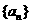 的前
的前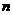 项和
项和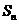 满足
满足 ,那么
,那么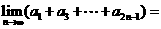 ( C )
( C )
A.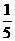 B.
B.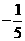 C.
C.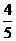 D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com