
题目列表(包括答案和解析)
19.(本小题满分12分)
已知数列{an}的前n项和为Sn(n∈N*),点(an,Sn)在直线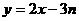 上.
上.
(Ⅰ)求证:数列{an+3}是等比数列;Ⅱ)求数列{an}的通项公式;(Ⅲ)数列{an}中是否存在成等比数列的三项?若存在,求出一组合适条件的三项;若不存在,说明理由.
18.(本小题满分12分)
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥平面ABCD,且SA=SB,点E为AB的中点,点F为SC的中点.
 (Ⅰ)求证:EF⊥CD;
(Ⅰ)求证:EF⊥CD;
(Ⅱ)求证:平面SCD⊥平面SCE.
17.(本小题满分12分)在△ABC中,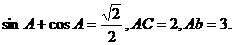
(Ⅰ)求 的值; (Ⅱ)求△ABC的面积.
的值; (Ⅱ)求△ABC的面积.
18. (本小题满分14分)
(本小题满分14分)
(Ⅰ)
证明:连结BD交AC于点O,连结EO.
 O为BD中点,E为PD中点,
O为BD中点,E为PD中点,
∴EO//PB. ……………………1分
 EO
EO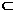 平面AEC,PB
平面AEC,PB 平面AEC,
……………………2分
平面AEC,
……………………2分
 ∴ PB//平面AEC.
……………………3分
∴ PB//平面AEC.
……………………3分
(Ⅱ)
证明: P点在平面ABCD内的射影为A,
P点在平面ABCD内的射影为A,
∴PA⊥平面ABCD.

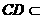 平面ABCD,
平面ABCD,
∴ .
……………………4分
.
……………………4分
又 在正方形ABCD中
在正方形ABCD中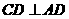 且
且 , ……………………5分
, ……………………5分
∴CD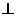 平面PAD.
……………………6分
平面PAD.
……………………6分
又
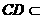 平面PCD,
平面PCD,
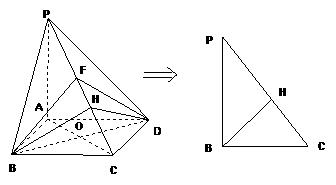
∴平面 平面
平面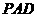 .
……………………7分
.
……………………7分
 (Ⅲ)
(Ⅲ)
解法一:过点B作BH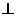 PC于H,连结DH.
……………………8分
PC于H,连结DH.
……………………8分
易证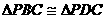 ,
, DH
DH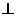 PC,BH=DH,
PC,BH=DH,
∴ 为二面角B-PC-D的平面角.
……………………10分
为二面角B-PC-D的平面角.
……………………10分
 PA⊥平面ABCD,
PA⊥平面ABCD,
∴AB为斜线PB在平面ABCD内的射影,
又BC⊥AB,
∴BC⊥PB.
又BH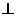 PC,
PC,
∴ ,
,
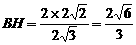 ,
……………………11分
,
……………………11分
在 中,
中,

=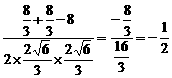 , ……………………12分
, ……………………12分
∴ 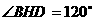 ,
……………………13分
,
……………………13分
∴二面角B-PC-D的大小为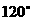 .
……………………14分
.
……………………14分
17.(本小题满分13分)
解:(Ⅰ) ,
,
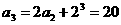 .
…………………………………2分
.
…………………………………2分
(Ⅱ)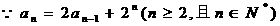 ,
,
∴ , …………………………………3分
, …………………………………3分
即 . …………………………………4分
. …………………………………4分
∴数列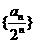 是首项为
是首项为 ,公差为
,公差为 的等差数列. …………5分
的等差数列. …………5分
(Ⅲ)由(Ⅱ)得
 ……………………………7分
……………………………7分
∴ .
……………………………8分
.
……………………………8分
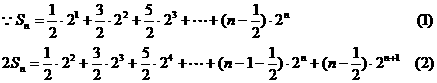
……………………………10分

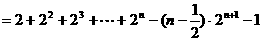
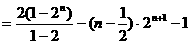
 .
.
∴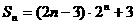 .
……………………………13分
.
……………………………13分
16.(本小题满分13分)
解:(Ⅰ)由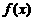 是R上的奇函数,有
是R上的奇函数,有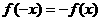 ,
…………………………1分
,
…………………………1分
即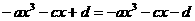 ,所以
,所以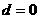 .
.
因此 .
…………………………………2分
.
…………………………………2分
对函数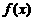 求导数,得
求导数,得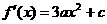 . ……………………………3分
. ……………………………3分
由题意得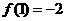 ,
,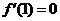 , ……………………………4分
, ……………………………4分
所以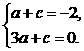 …………………………………5分
…………………………………5分
解得 ,
,
因此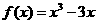 . …………………………………6分
. …………………………………6分
(Ⅱ)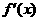
 .
………………………7分
.
………………………7分
令 >0,解得
>0,解得 <
< 或
或 >
>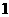 ,
,
因此,当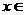 (-∞,-1)时,
(-∞,-1)时,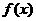 是增函数;
是增函数;
当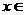 (1,+∞)时,
(1,+∞)时,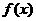 也是增函数. …………………………………8分
也是增函数. …………………………………8分
再令 <0,
解得
<0,
解得 <
< <
<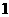 ,
,
因此,当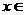 (-1,1)时,
(-1,1)时,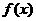 是减函数. ……………………………9分
是减函数. ……………………………9分
(Ⅲ)令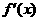 =0,得
=0,得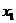 =-1或
=-1或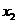 =1.
=1.
当 变化时,
变化时,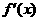 、
、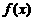 的变化如下表.
的变化如下表.
 |
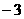 |
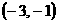 |
-1 |
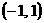 |
1 |
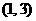 |
3 |
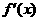 |
|
+ |
0 |
- |
0 |
+ |
|
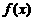 |
 |
↗ |
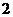 |
↘ |
 |
↗ |
18 |
…………………………………11分
从上表可知,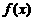 在区间
在区间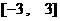 上的最大值是18 .
上的最大值是18 .
原命题等价于m大于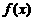 在
在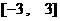 上的最大值,
上的最大值,
∴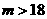 . …………………………………13分
. …………………………………13分
15.(本小题满分12分)
解:(Ⅰ)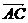 =
=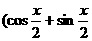 ,
, ,
,
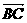 =
= ,
,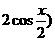 .
…………………………………2分
.
…………………………………2分
(Ⅱ)
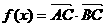
=  …………4分
…………4分
= 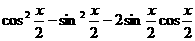
= 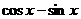 …………………………………6分
…………………………………6分
= 
= …………………………………8分
…………………………………8分
∴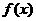 的最小正周期
的最小正周期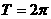 .
…………………………………9分
.
…………………………………9分
(Ⅲ)∵ 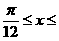
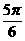 , ∴
, ∴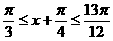 .
.
∴ 当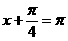 ,即
,即 =
=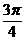 时,
时,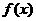 有最小值
有最小值 , ………………11分
, ………………11分
当 ,即
,即 =
=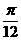 时,
时,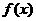 有最大值
有最大值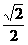 . ……………12分
. ……………12分
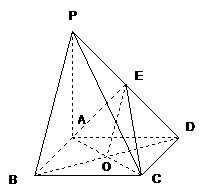
18.(本小题满分14分)
如图,在四棱锥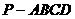 中,四边形
中,四边形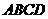 为正方形,
为正方形,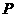 点在平面
点在平面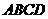 内的射影为
内的射影为 ,且
,且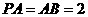 ,
, 为
为 中点.
中点.
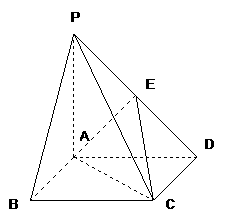 (Ⅰ)证明:
(Ⅰ)证明: //平面
//平面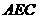 ;
;
(Ⅱ)证明:平面 平面
平面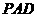 ;
;
(Ⅲ)求二面角 的大小.
的大小.
17.(本小题满分13分)
已知数列{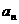 }满足
}满足 ,且
,且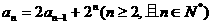 .
.
(Ⅰ)求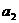 ,
,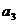 ;(Ⅱ)证明数列{
;(Ⅱ)证明数列{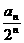 }是等差数列;(Ⅲ)求数列{
}是等差数列;(Ⅲ)求数列{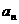 }的前
}的前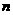 项之和
项之和 .
.
16.(本小题满分13分)
已知函数 是
是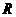 上的奇函数,当
上的奇函数,当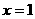 时,
时,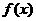 取得极值
取得极值 .
.
(Ⅰ)求函数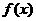 的解析式; (Ⅱ)求
的解析式; (Ⅱ)求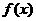 的单调区间;
的单调区间;
(Ⅲ)当
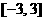 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com