
题目列表(包括答案和解析)
5.在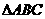 中,若
中,若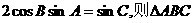 的形状一定是
的形状一定是
A.等腰直角三角形 B.等边三角形
C.直角三角形 D.等腰三角形
4.已知函数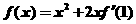 , 则
, 则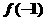 与
与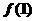 的大小关系是
的大小关系是
A、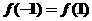 B、
B、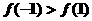 C、
C、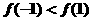 D、不能确定
D、不能确定
3. 在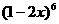 的展开式中
的展开式中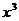 的系数是
的系数是
A.240 B.160 C.-160 D.-240
2.将函数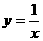 的图象按向量a平移后,得到
的图象按向量a平移后,得到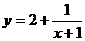 的图象,则
的图象,则
A.a=(1,2) B.a=(1,-2) C.a=(-1,2) D.a=(-1,-2)
1.已知不等式 的解集为A,函数
的解集为A,函数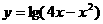 的定义或为B,则
的定义或为B,则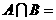
A.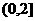 B.
B.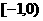 C.
C.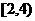 D.
D.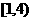
23.解:由f(x)是奇函数,得 b=c=0, (3分)
由|f(x)min|=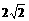 ,得a=2,故f(x)=
,得a=2,故f(x)= 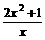 (6分)
(6分)
(2) 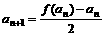 =
=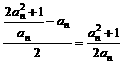 ,
,
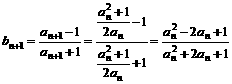 =
=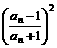 =
=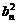 (8分)
(8分)
∴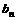 =
=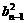 =
=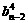 =…=
=…=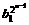 ,而b1=
,而b1=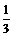
∴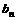 =
=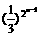 (10分)
(10分)
当n=1时, b1=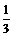 ,命题成立,
(12分)
,命题成立,
(12分)
当n≥2时
∵2n-1=(1+1)n-1=1+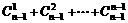 ≥1+
≥1+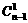 =n
=n
∴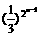 <
<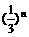 ,即 bn≤
,即 bn≤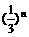 .
(14分)
.
(14分)
注:不讨论n=1的情况扣2分.
21.解:(Ⅰ) 证明:∵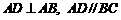 ,∴
,∴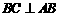 .……………………………1分
.……………………………1分
∵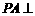 底面
底面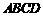 ,∴
,∴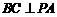 .………………………………………2分
.………………………………………2分
又∵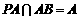 ,∴
,∴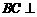 平面
平面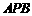 .…………………………………3分
.…………………………………3分
∵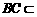 平面
平面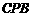 ,∴平面
,∴平面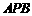
 平面
平面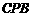 .…………………………4分
.…………………………4分
(Ⅱ) 解:作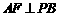 ,垂足为
,垂足为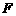 .
.
∵平面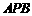
 平面
平面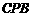 ,平面
,平面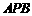
 平面
平面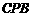
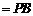 ,
,
∴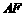
 平面
平面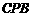 .
.
作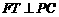 ,垂足为
,垂足为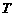 ,连结
,连结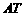 ,由三垂线定理,得
,由三垂线定理,得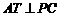 ,
,
∴ 是二面角
是二面角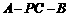 的平面角.………………………………6分
的平面角.………………………………6分
∵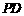 与底面
与底面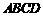 成
成 角,∴
角,∴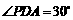 .
.
∴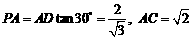 .
.
∴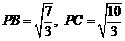 .
.
在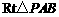 中,
中,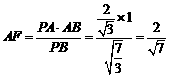 ,……………………7分
,……………………7分
在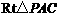 中,
中,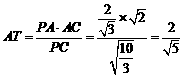 ,………………8分
,………………8分
∴在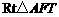 中,
中,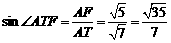 .
.
因此,二面角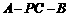 的平面角为
的平面角为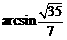 .…………………9分
.…………………9分
(Ⅲ) 设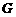 、
、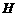 分别为
分别为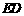 、
、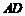 的中点,连结
的中点,连结 、
、 、
、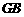 ,则
,则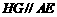 .
.
∵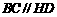 ,且
,且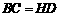 ,∴四边形
,∴四边形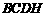 为平行四边形,∴
为平行四边形,∴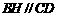 .
.
∴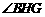 或它的补角就是异面直线
或它的补角就是异面直线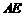 与
与 所成角.……………11分
所成角.……………11分
∵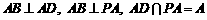 ,∴
,∴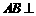 平面
平面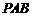 .
.
又∵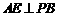 ,∴
,∴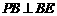 .
.
∵ ,∴
,∴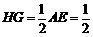 .
.
∵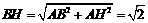 ,
,
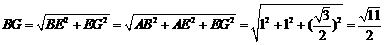 ,12分
,12分
∴在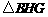 中,
中,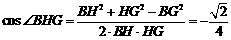 .…………13分
.…………13分
因此,异面直线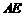 与
与 所成角为
所成角为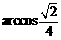 .……………………14分
.……………………14分
22解:(Ⅰ) 直线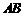 的方程为
的方程为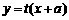 .………………………………………2分
.………………………………………2分
由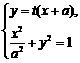 得
得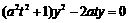 .…………………………3分
.…………………………3分
∴ 或
或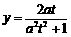 ,即点
,即点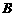 的纵坐标为
的纵坐标为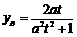 .…………4分
.…………4分
∵点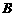 与点
与点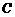 关于原点
关于原点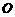 对称,
对称,
∴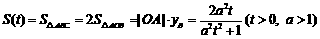 .…………6分
.…………6分
(Ⅱ) 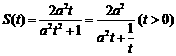 .
.
当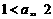 时,
时, ,
,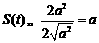 ,
,
当且仅当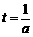 时,
时,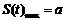 .……………………………………9分
.……………………………………9分
当 时,可证
时,可证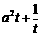 在
在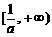 上单调递增,且
上单调递增,且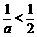 ,
,
∴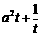 在
在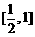 上单调递增.
上单调递增.
∴ 在
在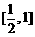 上单调递减.
上单调递减.
∴当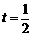 时,
时,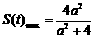 .…………………………………13分
.…………………………………13分
综上可得,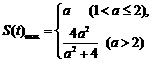 .…………………………14分
.…………………………14分
20.(1)令红色球为x个,则依题意得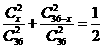 ,
(3分)
,
(3分)
所以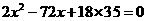 得x=15或x=21,又红色球多于白色球,所以x=21.所以红色球为21个,白色球为15个.
( 6分)
得x=15或x=21,又红色球多于白色球,所以x=21.所以红色球为21个,白色球为15个.
( 6分)
(2)设从袋中任取3个小球,至少有一个红色球的事件为A,均为白色球的事件为B,
则P(B)=1--P(A)=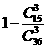 =
=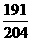 (12分)
(12分)
(13)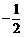 (14) (0,1)
(15)5 (16) --1 (17) (-∞,1]( 18 )③、④
(14) (0,1)
(15)5 (16) --1 (17) (-∞,1]( 18 )③、④
19.解: 由sinA(sinB+cosB)-sinC=0,得sinA(sinB+cosB)-sin(A+B)=0
所以 sinAsinB+sinAcosB-sinAcosB-cosAsinB=0
即 sinB(sinA-cosA)=0
因为 B∈(0,π),所以sinB≠0,从而cosA=sinA
由 A∈(0,π),知A=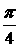 ,从而B+C=
,从而B+C=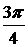
由sinB+cos2C=0得sinB+cos2(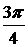 -B)=0
-B)=0
即 sinB-sin2B=0,亦即sinB-2sinBcosB=0
由此得 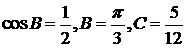
所以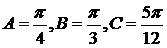
23.设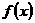 =
=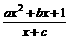 (a>0)为奇函数,且
(a>0)为奇函数,且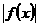 min=
min=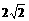 ,数列{an}与{bn}满足如下关系:a1=2,
,数列{an}与{bn}满足如下关系:a1=2, 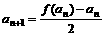 ,
,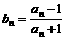 .
.
(1)求f(x)的解析表达式;(2) 证明:当n∈N+时, 有bn
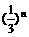 .
.
答案:一.选择题:每小题5分,共60分.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com