

题目列表(包括答案和解析)
3、函数y=2cos2x+1,(x∈R)的最小正周期为
1、设集合A={x|x-1<0,x∈R},B={x|x2+x-6<0,x∈R},则A∩B=
|
21. (本小题满分16分)
若定义在区间D上的函数y=f(x)对于区间D上的任意两个值x1、x2总有以下不等式≤f()成立,则称函数y=f(x)为区间D上的凸函数.
(1)证明:定义在R上的二次函数f(x)=ax2+bx+c(a<0)是凸函数;
(2)设f(x)=ax2+x(a∈R,a≠0),并且x∈[0,1]时,f(x)≤1恒成立,求实数a的取值范围,并判断函数f(x)=ax2+x(a∈R,a≠0)能否成为R上的凸函数;
(3)定义在整数集Z上的函数f(x)满足:
①对任意的x,y∈Z,f(x+y)=f(x)f(y);
②f(0)≠0,f(1)=2.
试求f(x)的解析式;并判断所求的函数f(x)是不是R上的凸函数说明理由.
盱眙中学2007届第二学期高三数学周练(五)
20.(本小题满分14分)
已知点集 ,其中
,其中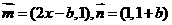 ,又知点列
,又知点列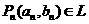 ,
,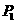 为
为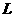 与
与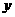 轴的的交点.等差数列
轴的的交点.等差数列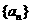 的公差为1,
的公差为1, .
.
(Ⅰ)求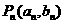 ;
;
(Ⅱ)若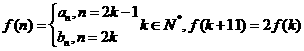 ,求出
,求出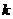 的值;
的值;
(Ⅲ)对于数列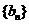 ,设
,设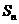 是其前
是其前 项和,是否存在一个与
项和,是否存在一个与 无关的常数
无关的常数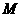 ,使
,使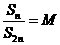 ,若存在,求出此常数
,若存在,求出此常数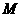 ,若不存在,请说明理由.
,若不存在,请说明理由.
19.(本小题满分14分)
在正方体ABCD-A1B1C1D1中,E是棱CC1的中点.
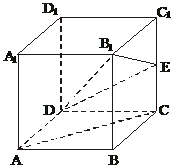
(1)判定AC与平面B1DE的位置关系,并证明;
(2)求证:平面B1DE⊥平面B1BD;
(3)求二面角B-B1E-D的大小.
18.(本小题满分14分)
已知直线 与双曲线
与双曲线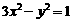 有A、B两个不同的交点.
有A、B两个不同的交点.
(1)如果以AB为直径的圆恰好过原点O,试求k的值;
(2)是否存在k,使得两个不同的交点A、B关于直线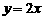 对称?试述理由.
对称?试述理由.
17.(本小题满分12分)
已知向量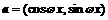 ,
,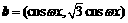 ,其中
,其中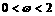 .记
.记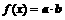 .
.
(1)若 的最小正周期为
的最小正周期为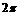 ,求函数
,求函数 的单调递增区间;
的单调递增区间;
(2)若函数 图象的一条对称轴的方程为
图象的一条对称轴的方程为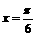 ,求
,求 的值.
的值.
16.定义:设有限集合 ,
,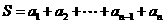 ,则
,则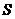 叫做集合
叫做集合 的模,记作
的模,记作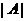 .若集合
.若集合 ,集合
,集合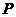 的含有三个元素的全体子集分别为
的含有三个元素的全体子集分别为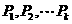 ,则
,则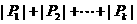 =__________(用数字作答).
=__________(用数字作答).
15、在公差为 的等差数列
的等差数列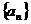 中,若
中,若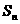 是
是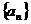 的前
的前 项和,则数列
项和,则数列 也成等差数列,且公差为
也成等差数列,且公差为 ,类比上述结论,相应地在公比为
,类比上述结论,相应地在公比为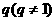 的等比数列
的等比数列 中,若
中,若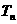 是数列
是数列 的前
的前 项积,则有=
项积,则有=
14. 如图,半径为2的半球内有一内接正六棱锥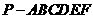 ,
,
则此正六棱锥的侧面积是________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com