
题目列表(包括答案和解析)
4.加强心理辅导
各种体育竞技,选手的过硬实力是首要,但临场的心态和意志是取得成功的关键.考场就如赛场,考生就是选手,当然,老师就是名副其实教练了.高考实际上就是考生在知识、能力、情感三维坐标上的大比拼.有人说,一个人事业的成功与否,“情商”比智商更重要.这里所说的“情商”包括意志品质、情感态度、心理承受能力以及交流交往能力等.可见情感意志不只是影响一个人的一场考试,甚至影响到一个人的终生.
能否攻克一道考题,有时只有一步之遥,或一念之差,有时是来自破题灵感,有时来自临场的心态意志.
参考文献:
① 柳柏濂.2006年高考广东卷数学试题和解答的分析.中学数学研究(广州),2006(12).
② 陈镇民.2006年广州市普通高中毕业班综合测试(二)数学试卷分析.2007(4)
③ 曾辛金.2006年广州市普通高中毕业班综合测试(一)数学试卷分析.2007(3)
④ 《2007年普通高等学校招生全国统一考试(文、理科)考试大纲的说明(广东卷)》
3. 加强培优扶差工作
6. 概率与统计
高中内容中的概率与统计,是大学统计学的基础,起着承上启下的作用,是每年高考命题的热点.排列、组合与概率是理科复习重点(等可能性事件、互斥事件、独立事件及几何概型).
5. 解析几何
解析几何的备考复习应当重视解题思路的开发、选择,讲究解题运算当中的方向、合理、
简明等算法算理.坐标法是研究几何问题的重要方法,建立坐标系,引入点的坐标,将几何问题化归为代数问题,用方程的观点实现几何问题的代数化解决,这是坐标思想的本质所在.
坐标法由曲线的方程来研究曲线的性质和给定条件求曲线的方程.熟练掌握直线和圆锥曲线
的标准方程、基本量与几何特征是正确解题的基石.平面几何的有关性质在解答某些解析几
何问题时,可以起到化繁为简的作用.
4. 函数与导数
由于函数与不等式的解答题是常规题、必考题,它的解答需要应用导数的有关知识,处于中档题或压轴题的位置.函数与不等式的复习既要依据课本中的重要知识点,还要适当选择难度较大、具有一定训练价值的新颖问题作为训练材料.求函数的单调性和单调区间、函数的最值可以应用导数法或定义法来解答.掌握求函数定义域、值域、解析式、的基本方法应十分熟练.同时,注意对换元、待定系数法等思想的运用.通过对分式函数、分段函数、复合函数、抽象函数等的学习,进一步体会函数关系的本质.促进函数思想在解题中的应用.
3.数列
数列既是高中数学的重要内容,又是学习高等数学的基础,它在高考中占有十分重要的地位.高考对数列的考查比较全面,等差数列、等比数列的考查是重点,递推数列试题是高考的热门话题,探索性问题是高考的热点,常在数列解答题中出现.
2.立体几何
由于立体几何解答题属于常规题、中档题,因而,立几的复习应紧扣考纲,熟练掌握课本中任一概念、每一定理的种种用途,突破画图、读图、用图的道道难关.在对问题的证明或计算时,一般需要将立体图形化归为平面图形. 空间位置关系(平行、垂直)、空间角(理科)、面积和体积仍然是立体几何考查的重点.
1.三角函数
由于三角解答题是基础题、常规题,属于容易题的范畴,因此,三角函数的复习应控制在
课本知识的范围和难度上.三角函数考查重点是三角函数的图象与性质、三角化简与求值以及三角形中的求值问题等.“正弦函数、余弦函数、正切函数的图象和性质”在复习中要求考生要能比较熟练地画出三角函数的图象,理解诸如周期、单调性、最值、对称中心、对称轴的相互关系等(也即 对函数
对函数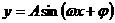 的图像变化的影响).解答三角函数高考题的一般策略是: (1)发现差异.观察角、函数运算间的差异,即所谓的“差异分析”.(2)寻找联系.运用相关三角公式,找出差异之间的内在联系.(3)合理转化.选择恰当的三角公式,促使差异的转化.三角恒等变形的一些具体通法是:常值代换,项的分拆与角的配凑,降幂与升幂,化弦(切)法,引入辅助角.
的图像变化的影响).解答三角函数高考题的一般策略是: (1)发现差异.观察角、函数运算间的差异,即所谓的“差异分析”.(2)寻找联系.运用相关三角公式,找出差异之间的内在联系.(3)合理转化.选择恰当的三角公式,促使差异的转化.三角恒等变形的一些具体通法是:常值代换,项的分拆与角的配凑,降幂与升幂,化弦(切)法,引入辅助角.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com