
题目列表(包括答案和解析)
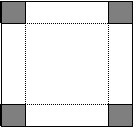
18.在边长为6的正方形纸板的四角切去相等的正方形,再沿虚线折起,做成一个无盖的方底箱子 (如图) ,
(1)当箱子容积最大时,切去的四个小正方形的边长恰为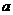 ,求出
,求出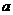 的值;
的值;
(2)若将切下来的四个小正方形再按相同方法做成四个无盖的方底箱子,问:当五个箱子的体积总和最大时, 第一次切下来的四个小正方形的边长是否仍然为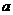 ?说明理由.
?说明理由.

17.甲乙两袋中装有大小相同的红球和白球,甲袋中装有1个红球和2个白球,乙袋中装有2个红球和1个白球,现从甲乙两袋中各取2个球;设取出的4个球中红球的个数为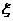 ,
,
(1)求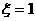 的概率;
的概率;
(2)写出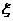 的分布列,并求出
的分布列,并求出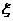 的数学期望值.
的数学期望值.
16.无穷等比数列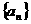 的各项都为正数,又
的各项都为正数,又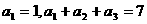 ;
;
(1)求数列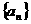 的通项公式;
的通项公式;
(2)取出数列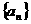 的前
的前
 项,设其中的奇数项之和为
项,设其中的奇数项之和为 ,偶数项之和为
,偶数项之和为 ;求出
;求出 和
和 的表达式(用
的表达式(用 表示).
表示).
15.已知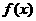 为定义在
为定义在 上的偶函数,当
上的偶函数,当 时,
时, 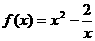 ;
;
(1)求 时,
时, 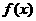 的解析式;
的解析式;
(2)求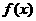 的值域.
的值域.
14.关于 的方程
的方程 有实根,那么实数
有实根,那么实数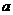 的取值范围为__________________.
的取值范围为__________________.
13.定义在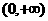 上的函数
上的函数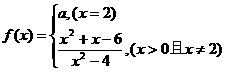 是
是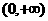 上的连续函数,那么
上的连续函数,那么 .
.
12.设数列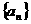 的通项
的通项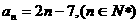 ,则
,则 .
.
11.已知集合 ,从
,从 到
到 的映射
的映射 满足:
满足:  中的任何元素都有原象,且
中的任何元素都有原象,且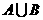 中的元素之和为124,求
中的元素之和为124,求 .
.
10.已知函数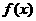 的导函数为
的导函数为 ,且对于任意
,且对于任意 ,总有
,总有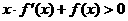 成立,那么
成立,那么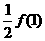 与
与 的大小关系为
的大小关系为
A.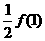 >
> B.
B.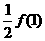 =
= C.
C.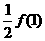 <
< D.不确定
D.不确定
9.设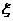 是离散型随机变量,
是离散型随机变量,  ,且
,且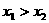 ,又已知
,又已知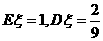 ,则
,则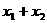 的值为
的值为
A.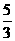 B.
B.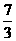 C.
C.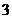 D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com