
题目列表(包括答案和解析)
18.(本小题满分14分)
某人作短期旅游,上午7时出发,乘电动自行车以匀速v千米/小时(4≤v≤20)从甲地到距50千米的乙地,然后换乘汽车以u千米/小时(30≤u≤100)匀速的自乙地向距300千米的丙地驶去,在同一天的下午4到9时到达丙地,设汽车、电动自行车所需时间分别是x,y小时.
(Ⅰ)图示满足上述条件的x+y的范围
(Ⅱ)如果已知所需的经费z=100+3(5-x)+2(8-y)(元,那么v,u分别是多少时走得最经济?此时需经费多少元?
17.(本小题满分12分)
如图已知△ABC是正三角形,PA⊥面ABC,且PA=AB=a,
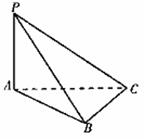 (Ⅰ)求PB与AC所成的角的大小;
(Ⅰ)求PB与AC所成的角的大小;
(Ⅱ)求二面A-PC-B的大小.
|
16.(本小题满分12分)
设a=(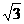 sinx,cosx),b=(cosx,cosx),若函数f(x)=a·b+m.(m∈R)
sinx,cosx),b=(cosx,cosx),若函数f(x)=a·b+m.(m∈R)
(Ⅰ)指出函数f(x)的最小正周期及单调递增区间;
(Ⅱ)当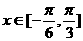 时,函数f(x)的最小值为2,求此函数f(x)的最大值,并求此时的x
时,函数f(x)的最小值为2,求此函数f(x)的最大值,并求此时的x
的值.
15.顶点在原点,焦点在直线3x-4y-12=0上的抛物线的标准方程是 .
14.函数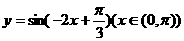 的单调递增区间是
.
的单调递增区间是
.
13.若向量a,b是非零向量,则“a·b<0”是“向量a,b的夹角为钝角”的 条件.
12.记Tn=a1·a2·…·an(n∈N*)表示n个数的积,其中ai为数列{an}中的第i项,若
an=2n-1,T4= .
11.先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有1,2,3,4,5,6)骰子朝上的点数分别为x,y,则logxy=1的概率是 .
10.已知向量a=(m,n),b=(cosθ,sinθ),其中m,n,θ∈R,若|a|=4|b|,则当a·b<λ2恒成立时,实数λ的取值范围是 ( )
A.λ>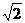 或λ<-
或λ<-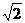 B.λ>
B.λ>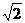 或λ<-2
或λ<-2
C.-2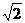 <λ<
<λ<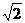 D.-2<λ<2
D.-2<λ<2
8.正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线AA1和BC的距离相等,
则动点P的轨迹是 ( )
A.线段 B.抛物线的一部分 C.双曲线的一部分 D.椭圆的一部分
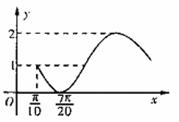 9.函数y=f(x)的图象如图所示,则y= f(x)的解析式是 ( )
9.函数y=f(x)的图象如图所示,则y= f(x)的解析式是 ( )
A.y=sin2x-2
B.y=2cos3x-1
C.y=sin(2x-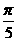 )+1
)+1
D.y=1-sin(2x-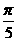 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com