
题目列表(包括答案和解析)
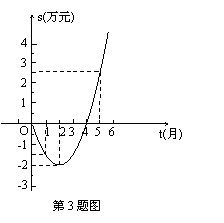
3. 某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程.下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).
根据图象提供的信息,解答下列问题:
(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关
系式;
(2)求截止到几月末公司累积利润可达到30万元;
(3)求第8个月公司所获利润是多少万元?
2.
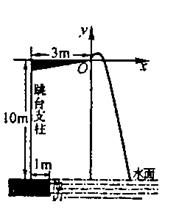 某跳水队员进行10米跳台跳水训练时,身体(看成一点)
某跳水队员进行10米跳台跳水训练时,身体(看成一点)
在空中的运动路线是如图所示坐标系下经过原点O的一条抛
物线,图中标出的数据为已知条件),在跳某个规定动作时,
正常情况下,该运动员在空中最高出距水面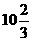 米,入水处
米,入水处
距池边的距离为4米,同时,运动员在距水面高度为5米以
前,必须完成规定的翻腾动作,并调整好入水姿势,否则就
会出现失误,
(1) 求这条抛物线的解析式;
(2)
在某次试跳中,测得运动员在空中调整好入水姿势时,距池边的水平距离为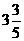 米,问此次跳水会不会失误并通过计算说明理由。
米,问此次跳水会不会失误并通过计算说明理由。
1. 一自动喷灌设备的喷流情况如图所示,设水管AB在高出地面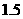 米的B处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头B与水流最高点C连线成
米的B处有一自动旋转的喷水头,一瞬间流出的水流是抛物线状,喷头B与水流最高点C连线成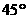 角,水流最高点C比喷头高
角,水流最高点C比喷头高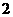 米,求水流落点D到A点的距离。
米,求水流落点D到A点的距离。
y
C 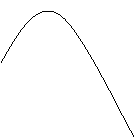

B
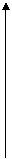
 A
D x
A
D x
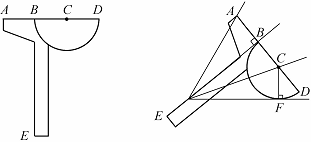
26、(本题满分14分)如图,Rt △OAC是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点C在y轴上,OC=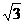 ,∠CAO=30º.将Rt △OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
,∠CAO=30º.将Rt △OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
⑴求折痕CE所在直线的解析式;
⑵求点D的坐标
⑶设点M为直线CE上的一点,过点M作AC的平行线,交y轴于点N,是否存在这样的点M,使得以M、N、D、C为顶点的四边形是平行四边形?若存在,请求出符合条件的点M的坐标;若不存在,请说明理由.
25、(本题满分12分)2005年4月20日发生在我市部分地区的大风冰雹灾害,使江都、宝应等县市8个乡镇、25万人受灾,当地政府已启动救灾应急预案,组织力量妥善安排受灾群众生活,各项抢险救灾工作正在紧张有序进行当中。一方有难八方支援,我市人民及时伸出了援助之手,迅速组织了一批救灾物资运往灾区。
这批物资若用n辆载重量为5吨的汽车装运,则会剩余21吨物资;若用n辆载重量为8吨的汽车装运,则有(n-1)辆汽车满载,最后一辆汽车不空,但所载物资不足5吨。⑴ 这批物资共有多少吨?
⑵ 已知载重量为5吨和8吨的汽车的租金分别为200元/辆、300元/辆, 若同时租用这两种汽车(每辆汽车都满载)共花费2600元, 则分别租用这两种汽车各多少辆?
⑶ 若同时使用载重量为5吨和8吨的两种汽车运输,请你设计一种方案,使每辆汽车都满载,且所需车辆数量最少。
24、(本题满分12分)
图(1)是一个10×10格点正方形组成的网格. △ABC是格点三角形(顶点在网格交点处), 请你完成下面两个问题:
(1) 在图(1)中画出与△ABC相似的格点△A1B1C1和△A2B2C2,
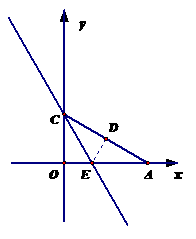
且△A1B1C1与△ABC的相似比是2, △A2B2C2与△ABC的相似比是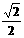 .
.
(2) 在图(2)中用与△ABC、△A1B1C1、△A2B2C2全等的格点三角形(每个三角形至少使用一次), 拼出一个你熟悉的图案,并为你设计的图案配一句贴切的解说词.
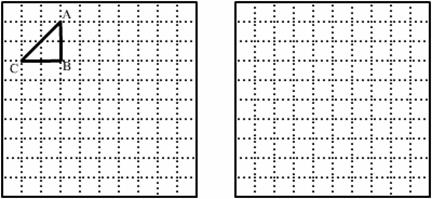
[解说词]
23、(本题满分12分)在足球比赛中,当守门员远离球门时,进攻队员常常使用“吊射”的战术(把球高高地挑过守门员的头顶,射入球门).一位球员在离对方球门30米的M处起脚吊射,假如球飞行的路线是一条抛物线,在离球门14米时,足球达到最大高度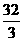 米。如图以球门底部为坐标原点建立坐标系,球门PQ的高度为2.44米.问:
米。如图以球门底部为坐标原点建立坐标系,球门PQ的高度为2.44米.问:
⑴ 通过计算说明,球是否会进球门?
⑵ 如果守门员站在距离球门2米远处,而守门员跳起后最多能摸到2.75米高处,他能否在空中截住这次吊射?
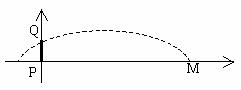
22、(本题满分12分) 三等分任意角是一个作图难题, 在距第一次提出这个问题两千年之后,这个问题才被证实用尺规作图(用没有刻度的直尺和圆规作图)无法解决. 现在有不少人创造了各种各样的辅助工具,用来解决尺规作图无法解决的三等分任意角的问题.
如图所示就是一个用来三等分任意角的工具及其使用示意图.
⑴ 制作该工具时BE所在的直线、点C应分别满足什么条件? 使用时应注意些什么?
⑵ 你能说出该工具三等分任意角的道理吗?
21、(本题满分10分)如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据:
⑴ 计算并完成表格;
转动转盘的次数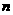 |
100 |
150 |
200 |
500 |
800 |
1000 |
落在“铅笔”的次数 |
68 |
111 |
136 |
345 |
564 |
701 |
落在“铅笔”的频率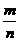 |
|
|
|
|
|
|
⑵ 请估计当n很大时,频率将会接近多少?
⑶ 假如你去转动该转盘一次,你获得可乐的概率是多少?在该转盘中,表示“可乐”区域的扇形的圆心角约是多少度?
⑷ 如果转盘被一位小朋友不小心损坏, 请你设计一个模拟实验方案(要求交代清楚替代工具和游戏规则).

20、(本题满分10分)如图, 在矩形ABCD中, 对角线AC、BD相交于点O.
⑴画出△AOB平移后的三角形, 其平移的方向为射线AD的方向, 平移的距离为线段AD的长(不写画法, 保留画图痕迹);
⑵在第⑴题画成功的图形中, 除了矩形ABCD外还有哪一种特殊的平行四边形? 并给予证明.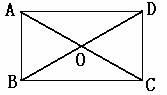
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com