
题目列表(包括答案和解析)
20、(14分)已知点H(-6,0),点P在Y轴的正半轴上,点Q在X轴的正半轴上,点M在直线PQ上,且满足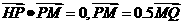 。
。
(1) 当点P在Y轴的正半轴上,点Q在X轴的正半轴上运动时,求点M的轨迹C的方程。
(2)若过点T(-2,0)作直线l与轨迹C交于A、B两点,则在X轴上是否存在一点E(m,0),使得⊿ABE为正三角形?若存在,求出直线l的方程;若不存在,说明理由?

19、(14分)已知点 都在直线:y=2x+2上,
都在直线:y=2x+2上,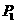 为直线l与x轴的交点,数列{
为直线l与x轴的交点,数列{ }是等差数列,公差为1。
}是等差数列,公差为1。
(1) 求数列{ }与{
}与{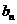 }的通项公式;
}的通项公式;
(2)
若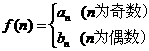 , 问是否存在
, 问是否存在
,若存在,求出k的值,若不存在,说明理由?
(3) 求证:
18、 (14分)如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AF=1,AB=
(14分)如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AF=1,AB= ,M是线段EF的中点。
,M是线段EF的中点。
(1)求证:MN//平面BDE; (2)求二面角A-DF-B的大小;
(3)试在线段AC上确定一点P,使得PF与CD所成的角是600
17、(12分)某车间在三天内,每天生产10件某产品,其中第一、二天分别生产出了1、2件次品,而质检部门每天要在生产的10件产品中随机地抽取4件进行检查,若发现有次品,则当天的产品不能通过。
(1) 求第一天通过的概率;(2)求前两天全部通过检查的概率;
(3)若厂内对车间生产的新产品采用记分制,两天全不通过记零分,通过一天、二天分别记1、2分,求该车间在这两天得分的数学期望。
16、(12分)已知锐角⊿ABC中,三内角A、B、C,两向量
 若
若 与
与 共线,
共线,
(1)
求角A的大小;(2)求函数 取最大值时,角B的值。
取最大值时,角B的值。
15、如图,在梯形ABCD中,M、N分别是AB,CD的中点,AB=2CD=4MN,将四边形MNCB沿MN将MNCB折成MN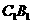 ,使二面角A-MN-
,使二面角A-MN-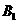 是直二面角,对于下列四个等式:
是直二面角,对于下列四个等式:
(1)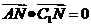 ,(2)
,(2) (3)
(3) ,(4)
,(4)
,则其中成立的序号为______________.
14、⊿ABC的外接圆半径R=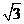 ,且满足
,且满足
13、 设
设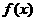 为偶函数,当
为偶函数,当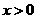 时,都有
时,都有

12、设各项均为实数的等比数列{ }的前n项的和
}的前n项的和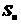 ,若
,若 ,
, ,则
,则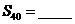 。
。
11、若椭圆 的一条准线经过抛物线
的一条准线经过抛物线 的焦点,若椭圆的左右焦点分别是
的焦点,若椭圆的左右焦点分别是 ,P为椭圆上的任一点,则三角形P
,P为椭圆上的任一点,则三角形P 的面积的最大值为_______.
的面积的最大值为_______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com