
题目列表(包括答案和解析)
5.坐标变换
坐标变换 在解析几何中,把坐标系的变换(如改变坐标系原点的位置或坐标轴的方向)叫做 坐标变换.实施坐标变换时,点的位置,曲线的形状、大小、位置都不改变,仅仅只改变点 的坐标与曲线的方程.
坐标轴的平移 坐标轴的方向和长度单位不改变,只改变原点的位置,这种坐标系的变换叫 做坐标轴的平移,简称移轴.
坐标轴的平移公式 设平面内任意一点M,它在原坐标系xOy中的坐标是(x,y),在新坐标系x ′O′y′中的坐标是(x′,y′).设新坐标系的原点O′在原坐标系xOy中的坐标是(h,k),则
(1)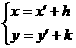 或
(2)
或
(2)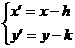
公式(1)或(2)叫做平移(或移轴)公式.
中心或顶点在(h,k)的圆锥曲线方程
中心或顶点在(h,k)的圆锥曲线方程见下表.
|
方 程 |
焦 点 |
焦 线 |
对称轴 |
|
|
椭 圆 |
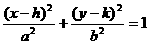 |
(±c+h,k) |
x=±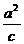 +h +h |
x=h y=k |
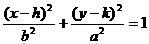 |
(h,±c+k) |
y=±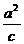 +k +k |
x=h y=k |
|
|
双曲线 |
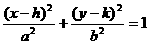 |
(±c+h,k) |
y=±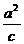 +k +k |
x=h y=k |
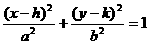 |
(h,±c+k) |
y=±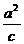 +k +k |
x=h y=k |
|
|
抛物线 |
(y-k)2=2p(x-h) |
(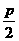 +h,k) +h,k) |
x=-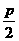 +h +h |
y=k |
|
(y-k)2=-2p(x-h) |
(-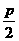 +h,k) +h,k) |
x=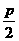 +h +h |
y=k |
|
|
(x-h)2=2p(y-k) |
(h, 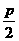 +k) +k) |
y=-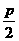 +k +k |
x=h |
|
|
(x-h)2=-2p(y-k) |
(h,- 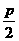 +k) +k) |
y=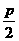 +k +k |
x=h |
4.圆锥曲线的统一定义
平面内的动点P(x,y)到一个定点F(c,0)的距离与到不通过这个定点的一条定直线l的距离之 比是一个常数e(e>0),则动点的轨迹叫做圆锥曲线.
其中定点F(c,0)称为焦点,定直线l称为准线,正常数e称为离心率.
当0<e<1时,轨迹为椭圆
当e=1时,轨迹为抛物线
当e>1时,轨迹为双曲线
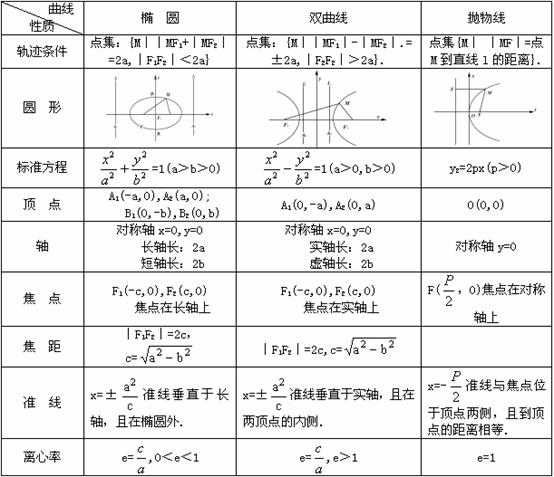
3.椭圆、双曲线和抛物线
椭圆、双曲线和抛物线的基本知识见下表.
2.圆
圆的定义
点集:{M||OM|=r},其中定点O为圆心,定长r为半径.
圆的方程
(1)标准方程
圆心在c(a,b),半径为r的圆方程是
(x-a)2+(y-b)2=r2
圆心在坐标原点,半径为r的圆方程是
x2+y2=r2
(2)一般方程
当D2+E2-4F>0时,一元二次方程
x2+y2+Dx+Ey+F=0
叫做圆的一般方程,圆心为(-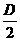 ,-
,-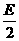 ),半径是
),半径是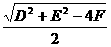 .配方,将方程x2+y2+Dx+Ey+F=0化为
.配方,将方程x2+y2+Dx+Ey+F=0化为
(x+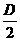 )2+(y+
)2+(y+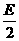 )2=
)2=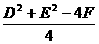
当D2+E2-4F=0时,方程表示一个点
(-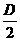 ,-
,-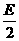 );
);
当D2+E2-4F<0时,方程不表示任何图形.
点与圆的位置关系 已知圆心C(a,b),半径为r,点M的坐标为(x0,y0),则
|MC|<r 点M在圆C内,
点M在圆C内,
|MC|=r 点M在圆C上,
点M在圆C上,
|MC|>r 点M在圆C内,
点M在圆C内,
其中|MC|=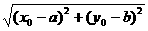 .
.
(3)直线和圆的位置关系
①直线和圆有相交、相切、相离三种位置关系
直线与圆相交?有两个公共点
直线与圆相切?有一个公共点
直线与圆相离?没有公共点
②直线和圆的位置关系的判定
(i)判别式法
(ii)利用圆心C(a,b)到直线Ax+By+C=0的距离d=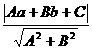 与半径r的大小关系来判定.
与半径r的大小关系来判定.
1.方程的曲线
在平面直角坐标系中,如果某曲线C(看作适合某种条件的点的集合或轨迹 )上的点与一个二元方程f(x,y)=0的实数解建立了如下的关系:
(1)曲线上的点的坐标都是这个方程的解;
(2)以这个方程的解为坐标的点都是曲线上的点.那么这个方程叫做曲线的方程;这条曲线叫 做方程的曲线.
点与曲线的关系 若曲线C的方程是f(x,y)=0,则点P0(x0,y0)在曲线C上 f(x0,y0)=0;
f(x0,y0)=0;
点P0(x0,y0)不在曲线C上 f(x0,y0)≠0
f(x0,y0)≠0
两条曲线的交点 若曲线C1,C2的方程分别为f1(x,y)=0,f2(x,y)=0,则
点P0(x0,y0)是C1,C2的交点
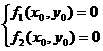
方程组有n个不同的实数解,两条曲线就有n个不同的交点;方程组没有实数解,曲线就没有 交点.
4.了解用坐标法研究几何问题的思想,初步掌握利用方程研究曲线性质的方法.
3.理解坐标变换的意义,掌握利用坐标轴平移化简圆锥曲线方程的方法.
2.掌握圆锥曲线的标准方程及其几何性质,并根据所给的条件画圆锥曲线,了解圆锥曲线的 一些实际应用.
1.掌握直角坐标系中的曲线与方程的关系和轨迹的概念,能够根据所给条件,选择适当的直 角坐标系求曲线的方程,并画出方程所表示的曲线.
8.已知圆C:x2+(y-1)2=5,直线l:mx-y+1=0,
(1)求证:对m∈R,直线l与圆C总有两个不同交点;
(2)设l与圆C交于A、B两点,若|AB|=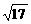 ,求l的倾斜角;
,求l的倾斜角;
(3)求弦AB的中点M的轨迹方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com