(七)平面与平面平行，平面与平面垂直

例7　 如图，在△ABC中，AD⊥BC，E为AD上的三 等分点，AE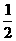＝ED，过E的直线MN∥BC，交AB、AC于M、N，将△AMN折起 到与平面MBCN成60°，求证：平面A′MN⊥平面A′BC.

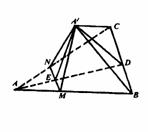
证明：∵AD⊥BC，BC∥MN

∴A′E和ED都垂直于MN，

∴∠A′ED是二面角A′MN-MN-MBCN的平面角， ∴∠A′ED＝60°，A′E＝AE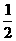＝ED＝ED·cos60°.

∴△A′ED是直角三角形，且A′E⊥A′D.

又∵A′E⊥MN，MN∥BC，

∴A′E⊥BC，而BC∩A′D＝D.

∴A′E⊥平面A′BC，

∵A′E面A′MN，

∴平面A′MN⊥平面A′BC.

(六)异面直线所成的角、直线与平面所成的角

例6　 如图，四面体OABC中，OA、OB、OC两两垂直， ∠OBA=45°,∠OBC=60°，M为AB的中点，求：

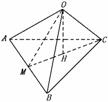
(1)BC与平面OAB所成的角；

　(2)OC与平面ABC所成的角。

解　 (1)因OC⊥OB，OC⊥AO，AO∩BO=0，

故 OC⊥面OAB。

故 ∠OBC为BC与平面OAB所成的角。

由已知∠OBC=60°，即为所求。

(2)因OA⊥OB，∠ABO=45°，M为AB中点

则 OM⊥AB，而OC⊥AB，OC∩OM=O

所以 AB⊥面OMC，而AB面OAB，

所以 面OAB⊥面OMC，

过O作OH⊥MC于H，则OH⊥面ABC

故 ∠OCM为OC与面ABC所成的角。

设OA＝a,则OM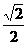＝a

又OB＝a,则OC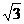＝a，

tg∠OCM==,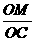

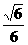所以 ∠OCM=arctg.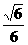

(五)三垂线定理及逆定理

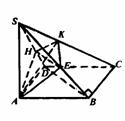
例5　 已知：如图，S为 正方形ABCD所在平面外一点，SA⊥平面ABCD，过A作截面 AEKH⊥SC.

求证：AE⊥SB，AH⊥SD，AK⊥HE.

证明：

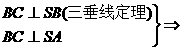
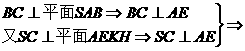
AE⊥平面SBC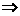AE⊥SB.

同理可证AH⊥平面SDC，故AH⊥SD.又∵ABCD为正方形，∴Rt△SAD≌Rt△SAB.故SD＝SB，SH＝SE.

∴HE∥DB.SA⊥DB，则SA⊥HE，SK⊥平面AEKH，AK是SA在截面上的射影，故HE⊥AK(三垂线定 理的逆定理).

(四)直线平面垂直的判定与性质定理

例4　 如图，△ABC为等腰三角形，其顶角A为钝角， D为底边BC的中点，DE、D F分别垂直于两腰AB和AC，沿DE和DF将△BDE和△CDF折起，恰好使得BD和CD重合，设B、C重 合于B′点，求证：AB′⊥面AEDF.

证明　 因DE⊥AB，

则 DE⊥B′E，AB∩B′E=E.

故 DE⊥面B′EA

又因 B′AB′EA

故 B′A⊥ED

同理，B′A⊥BF，则ED∩DF=D，

所以 B′A⊥面AEDF.

(三)直线与平面平行的判定与性质定理

例3　 直角△ABC的一条边AB∩α＝A，另一边BC不在平面α内，若∠ABC在 α上的射影仍是直角，求证BC∥α.

证明：如图，过B、C分别作α的垂线，垂足分别为B′、C′，则∠AB′C′是∠ABC在α上的射影.

∴∠AB′C′＝90°

又∵BB′⊥α，AB′α，B′C′α，

∴AB′⊥BB′，C′B′⊥BB′.

∵B′A∩BB′＝B′，

∴C′B′⊥平面AB′B.

∵B′C′∩B′B＝B′，

∴AB′⊥平面BB′C′C.

∵BC面BB′C′C，

∴BC⊥AB′.

∵∠ABC＝90°，AB∩AB′＝A，

∴BC⊥平面ABB′.

∴BC∥B′C′.

∴BC∥α.

(二)异面直线，两直线的位置关系，证明两直线异面、平行的一般方法

例2　 已知如图，a∥α,a∥β,α∥β,α∩β=b.求证：a∥b.

证明： 在α上任取一点A(Ab)，则a与点A确定了一个平面γ，γ∩α=c

因 a∥α,a?α,cα,

所以 a∥α,a?α,cα,

故 a∥c

同理，在β上任取一点B(Bb)，a与B确定了平面δ，δ∩β＝d，有a∥d

因 a∥c∥d,

则 cβ,dβ,

故 c∥β

又因 α∩β=b，

所以 c∥b,a∥b.

(一)平面的基本性质，证明直线共面的基本方

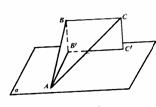
例1　 如图，ABCD-A₁B₁C₁D₁为正方体，E、F、G、H分别是棱AB、BC、CC₁、C₁D₁的中点.

求证：HG、EF、DC交于一点.

证明：∵E、F、G、H是正方体的棱AB、BC、CC₁、C₁D₁的中点，

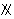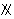∴直线EF面ABCD　 直线HG面CC₁D₁D，且直线EFCD，EFCD.

∴EF与CD、HG与CD必分别相交.

设EF∩CD于P，HG∩CD于P′，

由平几知识有△EBF≌△PCF，△P′GC≌△HC₁G.

∴PC＝BE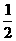＝AB，P′C＝C₁H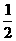＝C₁D₁

而正方体中AB＝C₁D₁

∴PC＝P′C，即P与P′重合.

∴HG、EF、DC交于一点.

16.异面直线的距离

(1)定义　 与两条异面直线都垂直相交的直线叫做两条异面直线的公垂线.两条异面直线的公 垂线在这两条异面直线间的线段的长度，叫做两条异面直线的距离.

任何两条确定的异面直线都存在唯一的公垂线段.

(2)求两条异面直线的距离常用的方法

①定义法　 根据题目所给的条件，找出(或作出)两条异面直线的公垂线段，再根据有关定 理、性质求出公垂线段的长.

此法一般多用于两异面直线互相垂直的情形.

②转化法　 转化为以下两种形式：线面距离　 面面距离

③等体积法

④最值法

⑤射影法

⑥公式法

15.平行平面的距离

(1)定义　 和两个平行平面同时垂直的直线，叫做这两个平行平面的公垂线.公垂线夹在两个 平行平面间的部分，叫做这两个平行平面的公垂线段.两个平行平面的公垂线段的长度叫做 这两个平行平面的距离.

(2)求平行平面距离常用的方法

①直接利用定义求证(或连或作)某线段为距离，然后通过解三角形计算之.

②把面面平行距离转化为线面平行距离，再转化为线线平行距离，最后转化为点线(面)距 离，通过解三角形或体积法求解之.

14.直线和平面的距离

(1)定义　 一条直线和一个平面平行，这条直线上任意一点到平面的距离，叫做这条直线和 平面的距离.

(2)求线面距离常用的方法

①直接利用定义求证(或连或作)某线段为距离，然后通过解三角形计算之.

②将线面距离转化为点面距离，然后运用解三角形或体积法求解之.

③作辅助垂直平面，把求线面距离转化为求点线距离.