
题目列表(包括答案和解析)
6、设θ∈( ),则关于x,y的方程x2cscθ-y2secθ=1所表示的曲线是[ ]
),则关于x,y的方程x2cscθ-y2secθ=1所表示的曲线是[ ]
A. 实轴在y轴上的双曲线 B. 实轴在x轴上的双曲线
C. 长轴在y轴上的椭圆 D. 长轴在x轴上的椭圆
5、设一动点P到直线x=5的距离与它到点A(1,0)的距离之比为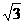 ,则动点P的轨迹方程是[ ]
,则动点P的轨迹方程是[ ]
A. 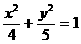 B.
B.
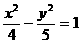
C. 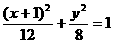 D.
D.
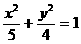
4、P是椭圆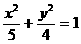 上的一点,F1和F2是焦点,若∠F1PF2=30°,则△F1PF2的面积等于[ ]
上的一点,F1和F2是焦点,若∠F1PF2=30°,则△F1PF2的面积等于[ ]
A. 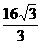 B.
B.
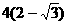 C.
C.  D. 16
D. 16
2、曲线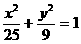 与曲线
与曲线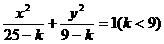 之间具有的等量关系:[ ]
之间具有的等量关系:[ ]
A. 有相等的长、短轴 B. 有相等的焦距
C. 有相等的离心率 D. 有相同的准线
2、如果方程x2+ky2=2表示焦点在y轴上的椭圆,则实数k的取值范围是[ ]
A. (0,+∞) B. (0,2) C. (1,+∞) D. (0,1)
1、如果椭圆的焦距、短轴长、长轴长成等差数列,则离心率e为[ ]
A. 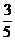 B.
B.
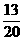 C.
C.
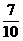 D.
D.
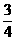
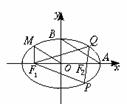
8.如图,从椭圆 =1(a>b>0)上一点M向x轴作垂线,恰好通过椭圆的左焦点F1,且它的长轴端点A及短轴的端点B的连线AB∥OM.
=1(a>b>0)上一点M向x轴作垂线,恰好通过椭圆的左焦点F1,且它的长轴端点A及短轴的端点B的连线AB∥OM.
(1)求椭圆的离心率e;
(2)设Q是椭圆上任意一点,F2是右焦点,求∠F1QF2的取值范围;
(3)设Q是椭圆上一点,当QF2⊥AB时,延长QF2与椭圆交于另一点P,若△F1PQ的面积为20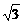 ,求此时椭圆的方程.
,求此时椭圆的方程.
7. 在面积为1的△PMN中,tanM=
在面积为1的△PMN中,tanM= ,tanN=-2,建立适当的坐标系,求以M、N为焦点且过点P的椭圆方程.
,tanN=-2,建立适当的坐标系,求以M、N为焦点且过点P的椭圆方程.
6.椭圆 =1(a>b>0),B(0,b)、B′(0,-b),A(a,0),F为椭圆的右焦点,若直线AB⊥
=1(a>b>0),B(0,b)、B′(0,-b),A(a,0),F为椭圆的右焦点,若直线AB⊥
B′F,求椭圆的离心率.
5.(2002年全国高考题)椭圆5x2+ky2=5的一个焦点是(0,2),那么k=_________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com