18、1)P()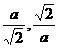

　　　 2)s (a)的值域为(0，)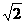

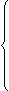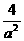
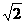　　　 3)　　　　　　　　　　　　　 a²－　　 <a≤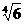

　　　 f (a)=min{g (a)， s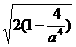(a)}=　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　 　　a>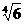

17.椭圆方程为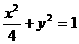；　 椭圆上点(-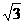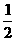，-)和(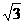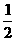，-)到P点的距离都等于。

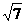16. x∈(60°，90°)∪(90°，120°)

15. 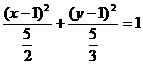，其中x、y不同时为零，轨迹是以(1，1)为中心，长短半轴分别为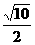和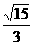，且长轴与x轴平行的椭圆，去掉坐标原点

13. 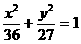除点(6，0)(-6，0)　 14. 1)　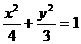　 2)cos∠F₁PF₂=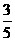

11. 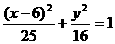　　　　12. 4或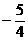

9. 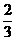　　　　　　　　　　　　　10.　　

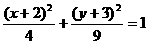
1. A　　 2. D　　 3. B　　 4. B　　 5. C　　 6. C　　 7. B　　 8. A

18、设椭圆C₁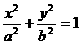：(a>b>0)，曲线C₂：y=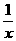，且C₁与C₂在第一象限内只有一个公共点P，(1)试用a表示P的坐标；(2)设A、B是椭圆C₁的两个焦点，当a变化时，求△ABP的面积，函数s (a)的值域；(3)证min{y₁，y₂……y_n}为y₁、y₂……y_n中最小的一个，设g (a)是以椭圆C₁的半焦距为边长的正方形的面积，试求函数f (a)=min{g(a)，s (a)}的表达式。

[一周一练答案]

17、设椭圆的中心是原点，长轴在x轴上，离心率e=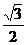，已知点P(0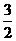，)到这个椭圆上的点的最远距离是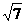，求这个椭圆方程，并求椭圆上到点P距离等于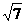的点的坐标。