
题目列表(包括答案和解析)
4.
若xÎ[-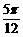 ,-
,-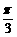 ],则y= tan(x+
],则y= tan(x+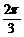 )-tan(x+
)-tan(x+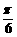 )+cos(x+
)+cos(x+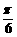 )的最大值是
(A)
)的最大值是
(A)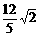 (B)
(B) (C)
(C)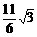 (D)
(D)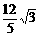
3.
过抛物线y2=8(x+2)的焦点F作倾斜角为60°的直线.若此直线与抛物线交于A,B两点,弦AB的中垂线与x轴交于P点,则线段PF的长等于
(A)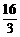 (B)
(B)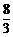 (C)
(C) (D)8
(D)8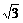
2. 设a, bÎR, ab≠0,那么,直线
ax-y+b=0和曲线 bx2+ay2=ab 的图形是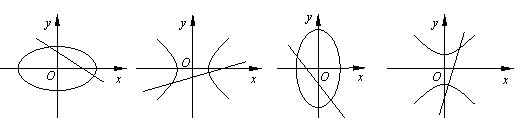
 (A)
(B)
(C) (D)
(A)
(B)
(C) (D)
1. 删去正整数数列1,2,3,……中的所有完全平方数,得到一个新数列.这个新数列的第2003项是 (A)2046 (B)2047 (C)2048 (D)2049
(17)(本小题满分12分)
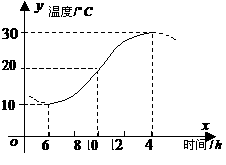
如图,某地一天从6时至14时的温度变化曲线近似满足函数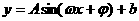 。
。
(Ⅰ)求这段时间的最大温差;
(Ⅱ)写出这段曲线的函数解析式。
(18)(本小题满分12分)
甲、乙两物体分别从相距70 的两处同时运动。甲第1分钟走2
的两处同时运动。甲第1分钟走2 ,以后每分钟比前1分钟多走1
,以后每分钟比前1分钟多走1 ,乙每分钟走5
,乙每分钟走5 。
。
(Ⅰ)甲、乙开始运动后几分钟相遇?
(Ⅱ)如果甲、乙到达对方起点后立即折反,甲继续每分钟比前1分钟多走1 ,乙继续每分钟走5
,乙继续每分钟走5 ,那么开始运动几分钟后第二次相遇?
,那么开始运动几分钟后第二次相遇?
(19)(本小题满分12分)
四棱锥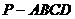 的底面是边长为
的底面是边长为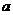 的正方形,
的正方形,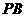
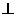 面
面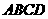 。
。
(Ⅰ)若面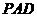 与面
与面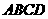 所成的二面角为
所成的二面角为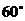 ,求这个四棱锥的体积;
,求这个四棱锥的体积;
(Ⅱ)证明无论四棱锥的高怎样变化,面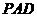 与面
与面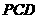 所成的二面角恒大于
所成的二面角恒大于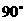 。
。
(20)(本小题满分12分)
设函数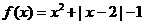 ,
,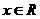 。
。
(Ⅰ)判断函数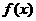 的奇偶性;
的奇偶性;
(Ⅱ)求函数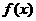 的最小值。
的最小值。
(21)(本小题满分14分)
已知点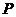 到两个定点
到两个定点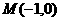 、
、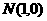 距离的比为
距离的比为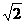 ,点
,点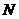 到直线
到直线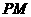 的距离为1。求直线
的距离为1。求直线 的方程。
的方程。
(22)(本小题满分12分,附加题满分4分)
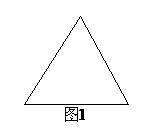
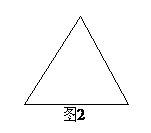
(Ⅰ)给出两块相同的正三角形纸片(如图1,图2),要求用其中一块剪拼成一个正三棱锥模型,另一块剪拼成一个正三棱柱模型,使它们的全面积都与原三角形的面积相等,请设计一种剪拼方法,分别用虚线标示在图1、图2中,并作简要说明;
(Ⅱ)试比较你剪拼的正三棱锥与正三棱柱的体积的大小;
(Ⅲ)(本小题为附加题,如果解答正确,加4分,但全卷总分不超过150分。)
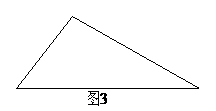
如果给出的是一块任意三角形的纸片(如图3),要求剪拼成直三棱柱模型,使它的全面积与给出的三角形的面积相等,请设计一种剪拼方法,用虚线标示在图3中,并作简要说明。
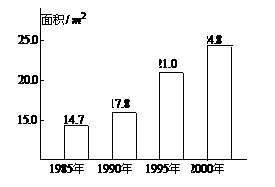
(13)。据新华社2002年3月12日电,1985年到2000年间,我国农村人均居住面积如图所示,其中,从 年到 年的五年间增长最快。
(14)函数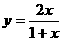
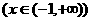 图象与其反函数图象的交点坐标为 。
图象与其反函数图象的交点坐标为 。
(15)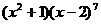 的展开式中
的展开式中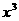 项的系数是
。
项的系数是
。
(16)对于顶点在在原点的抛物线,给出下列条件:
1焦点在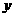 轴上;2焦点在
轴上;2焦点在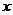 轴上;3抛物线上横坐标为1的点到焦点的距离为
轴上;3抛物线上横坐标为1的点到焦点的距离为 ;
;
4抛物线的通径的长为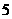 ;5由原点向过焦点的某条直线作垂线,垂足坐标为
;5由原点向过焦点的某条直线作垂线,垂足坐标为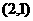 。
。
能使这抛物线方程为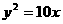 的条件是 。(要求填写合适条件的序号)
的条件是 。(要求填写合适条件的序号)
(1)若直线 与圆
与圆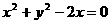 相切,则
相切,则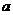 的值为
的值为
(A)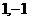 (B)
(B)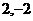 (C)
(C)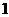 (D)
(D)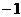
(2)复数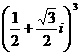 的值是
的值是
(A)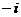 (B)
(B)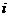 (C)
(C)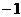 (D)
(D)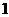
(3)不等式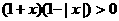 的解集是
的解集是
(A)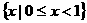 (B)
(B)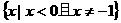 (C)
(C)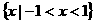 (D)
(D)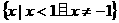
(4)函数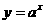 在
在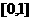 上的最大值与最小值的和为3,则
上的最大值与最小值的和为3,则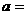
(A)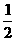 (B)
(B)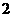 (C)
(C)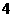 (D)
(D)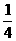
(5)在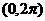 内,使
内,使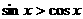 成立的
成立的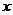 取值范围为
取值范围为
(A)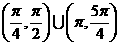 (B)
(B)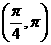 (C)
(C)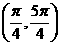 (D)
(D)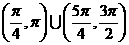
(6)设集合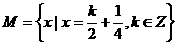 ,
,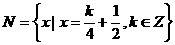 ,则
,则
(A)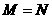 (B)
(B)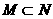 (C)
(C)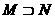 (D)
(D)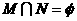
(7)椭圆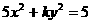 的一个焦点是
的一个焦点是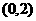 ,那么
,那么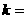
(A)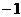 (B)
(B)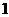 (C)
(C)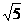 (D)
(D)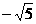
(8)一个圆锥和一个半球有公共底面,如果圆锥的体积恰好与半球的体积相等,那么这个圆锥截面顶角的余弦值是
(A)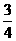 (B)
(B) (C)
(C)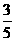 (D)
(D)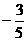
(9)已知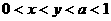 ,则有
,则有
(A)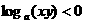 (B)
(B)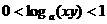 (C)
(C)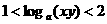 (D)
(D)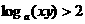
(10)函数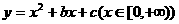 是单调函数的充要条件是
是单调函数的充要条件是
(A) (B)
(B)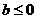 (C)
(C)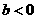 (D)
(D)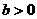
(11)设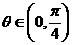 ,则二次曲线
,则二次曲线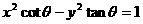 的离心率的取值范围为
的离心率的取值范围为
(A)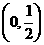 (B)
(B)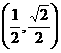 (C)
(C)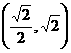 (D)
(D)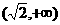
(12)从正方体的6个面中选取3个面,其中有2个面不相邻的选法共有
(A)8种(B)12种(C)16种(D)20种
(17)(本小题满分12分)
已知 ,
,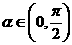 。求
。求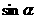 、
、 的值。
的值。
(18)(本小题满分12分)
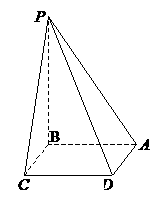
如图,正方形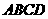 、
、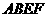 的边长都是1,而且平面
的边长都是1,而且平面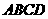 、
、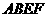 互相垂直。点
互相垂直。点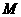
在 上移动,点
上移动,点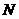 在
在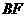 上移动,若
上移动,若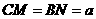
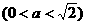 。
。
(Ⅰ)求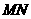 的长;
的长;
(Ⅱ)当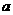 为何值时,
为何值时,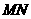 的长最小;
的长最小;
(Ⅲ)当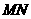 长最小时,求面
长最小时,求面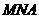 与面
与面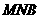 所成的二面角
所成的二面角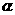 的大小。
的大小。
(19)(本小题满分12分)
设点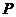 到点
到点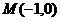 、
、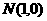 距离之差为
距离之差为 ,到
,到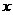 轴、
轴、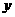 轴距离之比为
轴距离之比为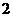 。
。
求 的取值范围。
的取值范围。
(20)(本小题满分12分)
某城市2001年末汽车保有量为30万辆,预计此后每年报废上一年末汽车保有量的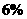 ,并且每年新增汽车数量相同。为保护城市环境,要求该城市汽车保有量不超过
,并且每年新增汽车数量相同。为保护城市环境,要求该城市汽车保有量不超过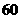 万量,那么每年新增汽车数量不应超过多少辆?
万量,那么每年新增汽车数量不应超过多少辆?
(21)(本小题满分12分)
设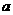 为实数,函数
为实数,函数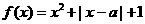 ,
,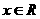 。
。
(Ⅰ)讨论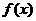 的奇偶性;
的奇偶性;
(Ⅱ)求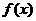 的最小值。
的最小值。
(22)(本小题满分14分)
设数列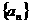 满足
满足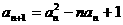 ,
,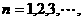
(Ⅰ)当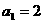 时,求
时,求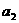 ,
,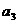 ,
,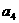 ,并由此猜想出
,并由此猜想出 的一个通项公式;
的一个通项公式;
(Ⅱ)当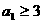 时,证明对所有的
时,证明对所有的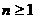 ,有
,有
(ⅰ)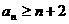 ;
;
(ⅱ)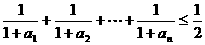 。
。
(13)函数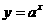 在
在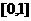 上的最大值与最小值的和为3,则
上的最大值与最小值的和为3,则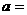 。
。
(14)椭圆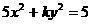 的一个焦点是
的一个焦点是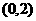 ,那么
,那么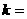 。
。
(15)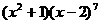 的展开式中
的展开式中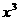 项的系数是
。
项的系数是
。
(16)已知函数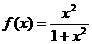 ,那么
,那么
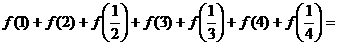 。
。
(1)圆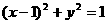 的圆心到直线
的圆心到直线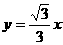 的距离是
的距离是
(A)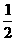 (B)
(B)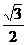 (C)
(C)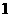 (D)
(D)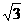
(2)复数 的值是
的值是
(A)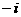 (B)
(B)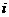 (C)
(C)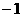 (D)
(D)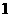
(3)不等式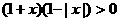 的解集是
的解集是
(A)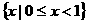 (B)
(B)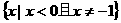 (C)
(C)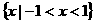 (D)
(D)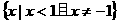
(4)在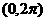 内,使
内,使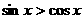 成立的
成立的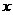 取值范围为
取值范围为
(A)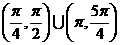 (B)
(B)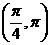 (C)
(C)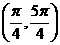 (D)
(D)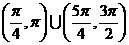
(5)设集合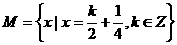 ,
,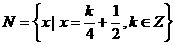 ,则
,则
(A)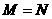 (B)
(B)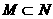 (C)
(C)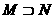 (D)
(D)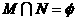
(6)点 到曲线
到曲线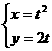 (其中参数
(其中参数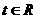 )上的点的最短距离为
)上的点的最短距离为
(A) (B)
(B)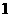 (C)
(C)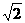 (D)
(D)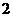
(7)一个圆锥和一个半球有公共底面,如果圆锥的体积恰好与半球的体积相等,那么这个圆锥截面顶角的余弦值是
(A)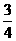 (B)
(B)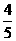 (C)
(C)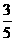 (D)
(D)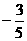
(8)正六棱柱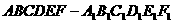 的底面边长为
的底面边长为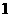 ,侧棱长为
,侧棱长为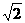 ,则这个棱柱的侧面对角线
,则这个棱柱的侧面对角线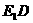 与
与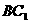 所成的角是
所成的角是
(A)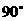 (B)
(B)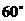 (C)
(C)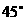 (D)
(D)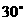
(9)函数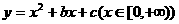 是单调函数的充要条件是
是单调函数的充要条件是
(A)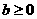 (B)
(B)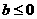 (C)
(C)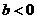 (D)
(D)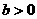
(10)函数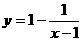 的图象是
的图象是
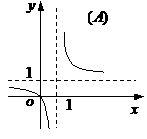
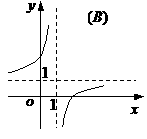
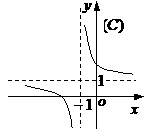
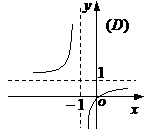
(11)从正方体的6个面中选取3个面,其中有2个面不相邻的选法共有
(A)8种(B)12种(C)16种(D)20种
(12)据2002年3月5日九届人大五次会议《政府工作报告》:“2001年国内生产总值达到95 933亿元,比上年增长7.3%.”如果“十·五”期间(2001年-2005年)每年的国内生产总值都按此年增长率增长,那么到“十·五”末我国国内年生产总值约为
(A)115 000亿元(B)120 000亿元(C)127 000亿元(D)135 000亿元
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com