
题目列表(包括答案和解析)
1. 关系分析法。即通过寻找关键词和关键量之间的数量关系的方法来建立问题的数学模型的方法。
例1. (水塔供水问题)某工厂有容量为300吨的水塔一个,每天从早上6时起到晚上10时止供应该厂生活和生产用水。已知该厂生活用水为每小时10吨,工业用水量W(吨)与时间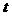 (单位:小时,定义早上6时
(单位:小时,定义早上6时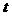 =0)的函数关系式为
=0)的函数关系式为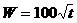 ,水塔的进水量有10级,第一级每小时进水10吨,以后每提高一级,每小时的进水量增加10吨,若某天水塔原有水100吨,在供水同时打开进水管。
,水塔的进水量有10级,第一级每小时进水10吨,以后每提高一级,每小时的进水量增加10吨,若某天水塔原有水100吨,在供水同时打开进水管。
(1)设进水量选用第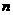 级,写出在
级,写出在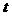 时刻水的存有量;
时刻水的存有量;
(2)问进水量选择第几级,既能保证该厂用水(水塔中水不空)又不会使水溢出。
读懂题目:题目涉及的关键词比较多:生活用水量、工业用水量、水的存有量、进水量、原有量。其数量关系为:存有量=进水量-用水量+原有量,而用水量=生活用水量+工业用水量。第一问的关键点是求“进水量选用第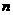 级”。第二问的关键点是“水塔中水不空不溢”转化为“存有量
级”。第二问的关键点是“水塔中水不空不溢”转化为“存有量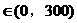 ”。
”。
建立数学模型: 存有量=进水量-用水量+原有量,而用水量=生活用水量+工业用水量=10
存有量=进水量-用水量+原有量,而用水量=生活用水量+工业用水量=10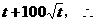 在选用第
在选用第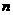 级的进水量时,
级的进水量时,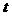 时刻水的存有量为
时刻水的存有量为 ,要使水搭中水不空不溢,则
,要使水搭中水不空不溢,则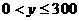 ,问题转化为确定
,问题转化为确定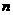 ,使
,使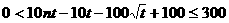 ,在(
,在(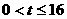 )上恒成立。
)上恒成立。
求解数学模型:面对上述不等式,如何求解?是否会转化为“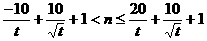 对一切
对一切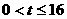 恒成立,”是否会作一个代换“令
恒成立,”是否会作一个代换“令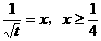 ”,将其转化为“
”,将其转化为“ 对一切
对一切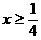 恒成立”,由于
恒成立”,由于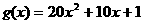 在
在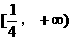 上的最小值为
上的最小值为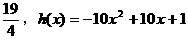 在
在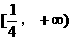 上的最大值为
上的最大值为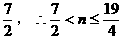 ,从而确定
,从而确定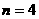 。
。
4. 检验。既要检验所得结果是否适合数学模型,又要评判所得结果是否符合实际问题的要求,从而对原问题作出合乎实际意义的回答。
3. 求解数学模型。根据所建立的数学模型,选择合适的数学方法,设计合理简捷的运算途径,求出数学问题的解,其中特别注意实际问题中对变量范围的限制及其他约束条件。
2. 建立数学模型。将实际问题抽象为数学问题,建模的直接准备就是审题的最后阶段从各种关系中找出最关键的数量关系,将此关系用有关的量及数字、符号表示出来,即可得到解决问题的数学模型。
数学建模分析的步骤:
1. 读懂题目。应包括对题意的整体理解和局部理解,以及分析关系、领悟实质。
“整体理解”就是弄清题目所述的事件和研究对象;
“局部理解”是指抓住题目中的关键字句,正确把握其含义;
“分析关系”就是根据题意,弄清题中各有关量的数量关系;
“领悟实质”是指抓住题目中的主要问题、正确识别其类型。
全国高中数学联赛模拟试题(一)
15. (20分)某新建商场设有百货部、服装部和家电部三个经营部,共有190名售货员,计划全商场的日营业额(每日卖出商品所收到的总金额)为60万元,根据经验,各部商品每1万元营业额需要售货员人数及每1万元营业额所得利润情况如表所示,商场将计划日营业额分配给三个经营部,同时适当安排各部的营业员人数,若商场预计每日的总利润为c万元,且19≤c≤19.7,又已知商场分配给经营部的营业额均为整数万元,问这个商场怎样分配营业额给三个部?各部分别安排多少名营业员?
|
部门 |
每1万元营业额需要售货员人数 |
每1万元营业额所得利润(万元) |
|
百货部 |
5 |
0.3 |
|
服装部 |
4 |
0.5 |
|
家电部 |
2 |
0.2 |
第二试
14. (20分)直线Ax+By+C=0(ABC≠0)与椭圆b2x2+a2y2=a2b2相交于P和Q两点,O为坐标原点,且OP⊥OQ,求证:.
13. (20分)求证:经过正方体中心的任意截面的面积不小于正方体一个侧面的面积.
12. 若实数a>0,则满足a5-a3+a=2的a值属于区间:①(0,);②(),③(,+∞);④(0,).其中正确的是_________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com