
题目列表(包括答案和解析)
7. 若 x的取值范围是( )
x的取值范围是( )
A. 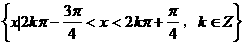
B. 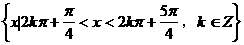
C. 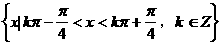
D. 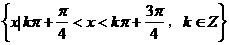
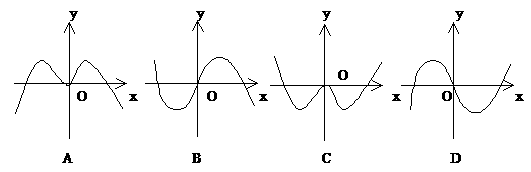
6. 函数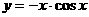 的部分图象是( )
的部分图象是( )
5. 若点P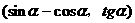 在第一象限,则在[0,2
在第一象限,则在[0,2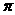 ]内
]内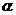 的取值范围是( )
的取值范围是( )
A. 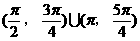
B. 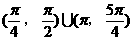
C. 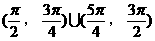
D. 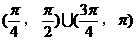
4. 函数 的最小值为( )
的最小值为( )
A. 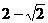 B.
B.
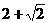
C. 0 D. 1
3. 函数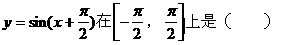
A. 增函数 B. 减函数
C. 偶函数 D. 奇函数
2. 下列函数中,以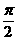 为周期的函数是( )
为周期的函数是( )
A. 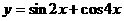
B. 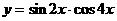
C. 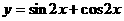
D. 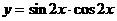
1. 函数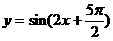 的图象的一条对称轴方程是( )
的图象的一条对称轴方程是( )
A. 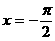 B.
B.
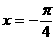
C. 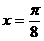 D.
D.
4. 基于上述几点理由,建议同学们在复习这部分内容时,做到“立足课本,落实三基;重视基础,抓好常规”即复习时以中低档题目为主,注意求值化简题以及求取值范围的习题,另外,注意充分利用单位圆,三角函数图象研究问题。
[典型例题分析与解答]
例1. 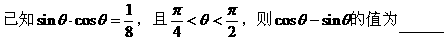
分析: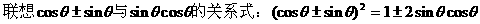
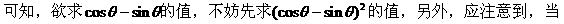
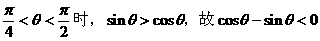
解: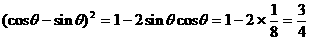
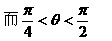
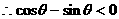
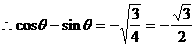
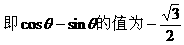
例2.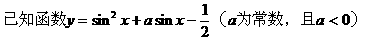
求函数的最小值。
分析:若将sinx换元,则函数转化为二次函数,从而可把三角函数的最值问题转化为二次函数的最值问题,但要注意到:转化后所得二次函数的定义域。
解: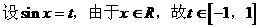
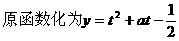
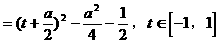
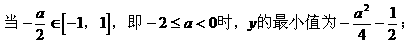

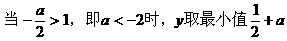
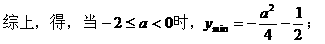
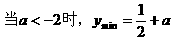
[注]在求解三角函数的最值时,注意三角函数的有界性。
例3. 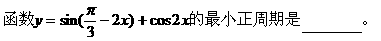
分析:一般地,要求三角函数的最小正周期,往往要用到如下结论:
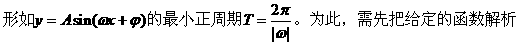 式通过三角公式,变形为上述结论中的函数形式,于是:
式通过三角公式,变形为上述结论中的函数形式,于是:
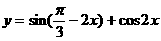
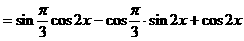
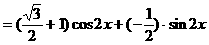
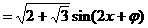
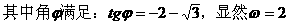

或按如下方法化简解析式:
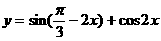
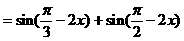
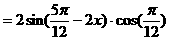
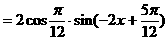
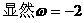

[注]一般地,如果给定的函数解析式不是形如y=Asin(ωx+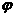 )的形式,在求其最小正周期时,往往先将解析式变形为y=Asin(ωx+
)的形式,在求其最小正周期时,往往先将解析式变形为y=Asin(ωx+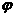 )的形式。
)的形式。
例4. 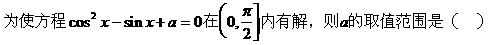


分析一:由方程形式,可把该方程采取换元法,转化为二次函数:设sinx=t,则原方

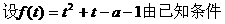
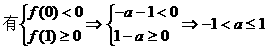
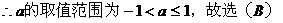
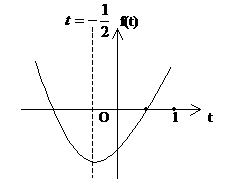
分析二: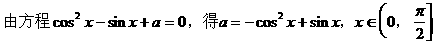
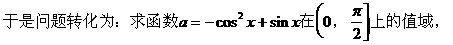
解法如下:
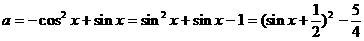
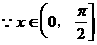
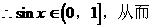
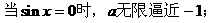
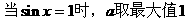
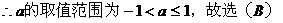
例5. 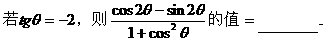
分析一:观察角,函数名称的关系后,易联想到万能公式,于是可以按照如下方式去求值。
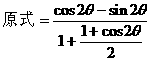
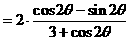
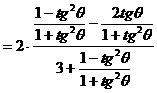
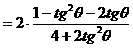
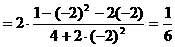
分析二:联想到关于sinθ,cosθ的齐次公式可以化切,于是可以按照如下方式求值。
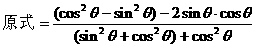
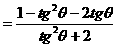
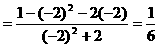
[注]两相比较,发现,解法二更为简捷,事实上,对于已知tgθ的值,而求关于sinθ,cosθ的齐次公式的值时,方法二更具有通用性。
例6. 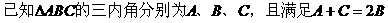
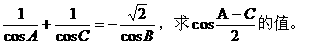
分析:这是一道以三角形为背景材料的三角函数问题,要注意题中的隐藏条件: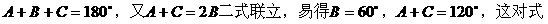

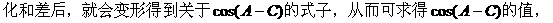
 的式子,从而立即求值。
的式子,从而立即求值。
解: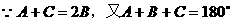
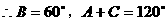
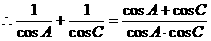
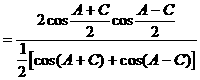

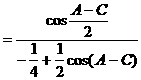
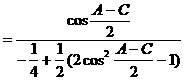
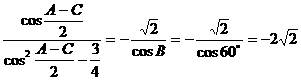
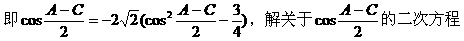
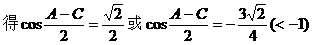

例7. 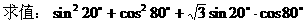
解法一:
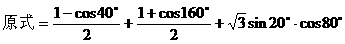
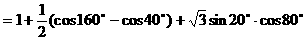
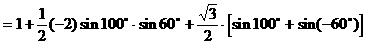
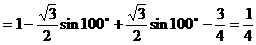
解法二: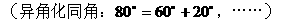
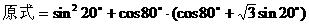
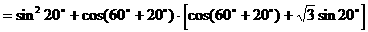
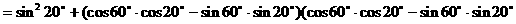

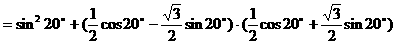
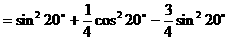
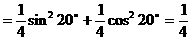
例8. 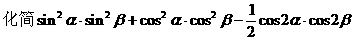
分析:对三角函数式化简的目标是:
(1)次数尽可能低;
(2)角尽可能少;
(3)三角函数名称尽可能统一;
(4)项数尽可能少。
观察欲化简的式子发现:
(1)次数为2(有降次的可能);
(2)涉及的角有α、β、2α、2β,(需要把2α化为α,2β化为β);
(3)函数名称为正弦、余弦(可以利用平方关系进行名称的统一);
(4)共有3项(需要减少),由于侧重角度不同,出发点不同,本题化简方法不止一种。
解法一: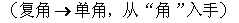
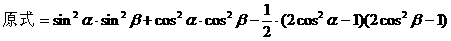
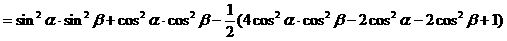
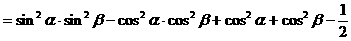
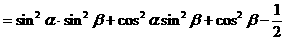
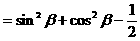
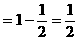
解法二:(从“名”入手,异名化同名)
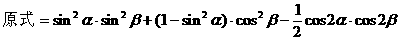
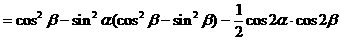
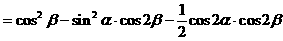
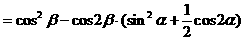
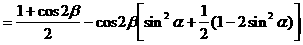
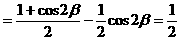
解法三:(从“幂”入手,利用降幂公式先降次)
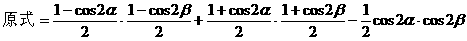
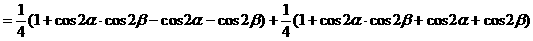
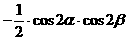
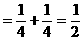
解法四:(从“形”入手,利用配方法,先对二次项配方)
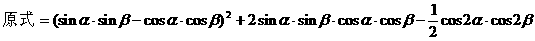

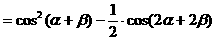
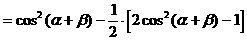
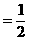
[注]在对三角式作变形时,以上四种方法,提供了四种变形的角度,这也是研究其他三角问题时经常要用的变形手法。
例9. 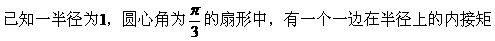 形ABCD,(如图),求该矩形的最大面积。
形ABCD,(如图),求该矩形的最大面积。
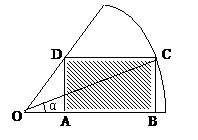
分析:欲求矩形的最大面积,按照函数的思想就是求面积函数的最大值,因此需要先依照题意,建立面积函数,选哪个量作自变量呢?经尝试发现:选取∠COB=α为面积函数的自变量最优,于是可建立一个以角α为自变量的三角函数来表示矩形面积,进而研究该函数的最值即可。
解: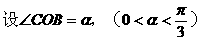
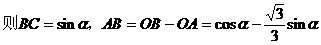
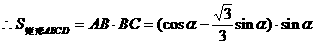
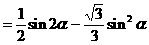
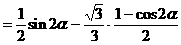
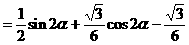



[模拟试题]
3. 三角恒等式的证明因其技巧性较强,一度成为数学的难点,近些年的高考试题对这类题目的考查在减少,要求有所降低,但我们应该充分重视三角变形,因为其中体现了对三角公式的运用能力,尤其体现了事物之间互相联系,互相转化的辩证思想。
2. 三角函数的周期性,以及y=sinx,y=cosx的有界性是试题经常考查的重要内容。要掌握形如y=Asin(ωx+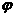 )或y=Acos(ωx+
)或y=Acos(ωx+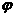 )的函数的周期的求法;灵活应用y=sinx,y=cosx的有界性研究某些类型的三角函数的最值(或值域)问题。
)的函数的周期的求法;灵活应用y=sinx,y=cosx的有界性研究某些类型的三角函数的最值(或值域)问题。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com