
题目列表(包括答案和解析)
7.三棱锥S-ABC中,SA、SB、SC两两垂直,则S在平面ABC上的射影为△ABC的________心。
6.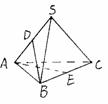 设三棱锥S-ABC中,SA、S B、SC两两垂直,
设三棱锥S-ABC中,SA、S B、SC两两垂直,
且SA=4,SB=3,SC=5,D为SA的中点,E为BC
的中点,则三棱锥B-AED的体积等于( )
A.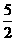 B.
B.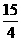
C.5 D.10
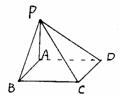
5.过正方形ABCD的顶点A,引PA⊥平面ABCD,
若PA=AB,则平面ABP和平面CDP所成的二面角
的大小是( )
A.30° B.45°
C.60° D.90°
4.正三棱锥S-ABC的底面边长为a,侧棱长为b,M
为AC的中点,N为BC的中点,过MN平行于SC的
平面在正三棱锥内的截面面积为( )
 A.
A.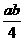 B.
B.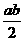 C.
C.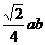 D.
D.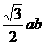
3.四面体的一条棱长是x,其余棱长都是1,则该四面体的体积最大时,x的值为( )
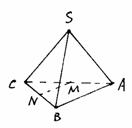 A.
A.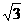 B.2
C.
B.2
C.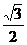 D.
D.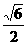

2.一个四棱锥的所有侧面与底面所成的角都是30°,若此棱锥的底面面积为S,则它的侧面面积等于( )
A.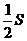
 B.
B.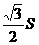 C.
C.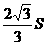 D.2S
D.2S
1.下列四个命题中,其本身与其逆命题都成立的是( )
A.正四棱柱一定是长方体 B.正方体一定是正四棱柱
C.直平行六面体一定是直四棱柱 D.侧棱与底面垂直的棱柱是直棱柱
20. (本小题满分12分)
(理科学生作)已知 二次函数f(x)=x2+ax+b (a,b ∈R)的定义域为[-1,1],且|f(x)|的最大值为M.
(Ⅰ)试证明|1+b|≤M;
(Ⅱ)试证明M≥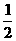 ;
;
(Ⅲ)当M=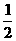 时,试求出f(x)的解析式.
时,试求出f(x)的解析式.
(文科学生作)设二次函数f(x)=ax2+bx+c (a,b,c∈R)
若x1<x2<x3<x4且x1+x4=x2+x3
(Ⅰ)试证 f(x1)+f(x4)=f(x1+x4)-2ax1·x4+c
(Ⅱ)试比较 x1·x4与x2·x3之间的大小关系.
(Ⅲ)试比较 f(x1)+f(x4)与f(x2)+f(x3)之间的大小关系.
19.(本小题满分16分)
已知 数列{an}中,a1>0,且an+1-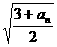
. (Ⅰ)试求a1的值,使得数列{an}是一个常数数列;
(Ⅰ)试求a1的值,使得数列{an}是一个常数数列;
(Ⅱ)试求a1的取值范围,使得an+1>an 对任何自然数n都成立;
(Ⅲ)若a1=4,设bn=| an+1-an|(n=1,2,3…),并以Sn表示数列{bn}的前n项的和,试证明:Sn<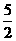 .
.
18.(本小题满分12分)
经市场调查分析知,某地明年从年初开始的前n个月,对某种商品需求总量f(n)(万件)
近似地满足下列关系:f(n)=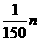 (n+1)(35-2n)
(n=1,2,3,…12)
(n+1)(35-2n)
(n=1,2,3,…12)
(Ⅰ)写出明年第n个月这种商品需求量g(n) (万件)与月份n的函数关系式,并求出哪几个月的需求量超过1.4万件;
(Ⅱ)若计划每月该商品的市场投放量都是p 万件,并且要保证每月都满足市场需求,则p至少为多少万件?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com