7．若不等式|x－4|+|3－x|<a的解集非空集，则a的取值范围是　　　　　　 (　 　)。

　 (A)(－∞, 1)　 (B)[1,　 +∞) (C)(1, +∞)　 (D)(3, 4)

6．若x, y∈R, x²－y²=4，则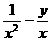的取值范围是　　　　　　　　　　　　 ( 　　)。

　 (A)(－∞, 0)∪(0, +∞)(B)(－1, 1)(C)(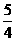－∞, ](D)(－∞, －2]∪[2, +∞)

5．已知x, y∈R, x²+y²+2x<0，则　　　　　　　　　　　　　　　　　　　 ( 　　)。

　 (A)x²+y²+6x+8<0　 (B)x²+y²+6x+8>0　 (C)x²+y²+4x+3<0　 (D)x²+y²+4x+3>0

4．不等式ax²+bx+2>0的解集是(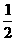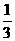－, ), 则a－b等于　　　　　　　　 ( 　　)。

　 (A)－4　 (B)14　 (C)－10　 (D)10

3．已知定义在R上的偶函数y=f(x)在[0, +∞)上为增函数，且f(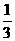)=0，则满足f(log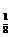x)>0的x的取值范围是　　　　　　　　　　　　　　　　　　　　　　　　　　 (　 　)。

　 (A)(0, 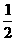)　 (B)(2, +∞)　 (C)(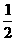, 1)∪(2, +∞)　 　(D)(0, 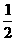)∪(2, +∞)

2．若不等式x²－log_ax<0在(0, 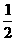)内恒成立，则a的取值范围是　　　　　 ( 　　)。

　 (A)[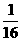, 1)　 (B)(1, +∞)　 (C)(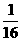, 1)　 (D)(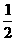, 1)∪(1, 2)

1．设实数x₁, x₂, ……,x_n的算术平均数是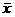，若a是不等于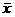的任意实数，并记p=(x₁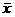－)²+(x₂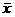－)²+……+(x_n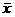－)²，q=(x₁－a)²+(x₂－a)²+……+(x_n－a)²，, 则一定有 ( 　　)。

　 (A)p=q　 (B)p>q　 (C)p≥q　 (D)p<q

有的应用题中还会出现多个不同数列相互之间的递推关系，对于该类问题，要正确处分没数列间的相互联系，整体考虑。

例4、甲乙两容器中分别盛有浓度为10%、20%的某种溶液500ml，同时从甲乙两个容器中取出100ml溶液，将近倒入对方的容器搅匀，这称为是一次调和，记a₁==10%,b₁=20%,经(n-1)次调和后甲、乙两个容器的溶液浓度为a­_n、b_n，

(1)试用a_n-1、b_n-1表示a­_n、b_n；

(2)求证数列 {a­_n-b_n}是等比数列，并求出a­_n、b_n的通项。

分析：该问题涉及到两个不同的数列a­_n和b_n，且这两者相互之间又有制约关系，所以不能单独地考虑某一个数列，而应该把两个数列相互联系起来。

解：(1)由题意

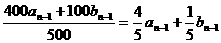a_n=；　　 b_n=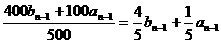

(2)a­_n-b_n=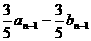=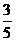(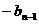)(n≥2)，∴{a­_n-b_n}是等比数列。又a₁-b₁=-10%,

∴a_n-b­n­=-10%(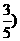^n-1.……(1)

又∵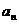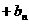==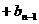…= a₁+b₁=30%，……(2)

联立(1)、(2)得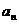=-(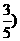^n-1·5%+15%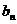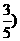；=(^n-1·5%+15%。

例3、某企业投资1千万元于一个高科技项目，每年可获利25%，由于企业间竞争激烈，每年底需要从利润中取出资金200万元进行科研、技术改造与广告投入，方能保持原有的利润增长率，问经过多少年后，该项目的资金可以达到或超过翻两番(4倍)的目标？(lg2=0.3)。

分析：设经过n年后，该项目的资金为a_n万元，则容易得到前后两年a_n和a_n-1之间的递推关系：a_n =a_n-1(1+25%)-200(n≥2)，对于这类问题的具体求解，一般可利用“待定系数法”：

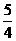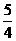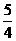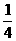解：由题，a_n =a_n-1(1+25%)-200(n≥2)，即a_n =a_n-1-200，设a_n +λ=(a_n-1+λ)，展开得a_n =a_n-1+λ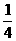，λ=-200，λ=-800，∴a_n -800=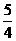(a_n-1-800)，即{a_n -800}成一个等比数列，a₁=1000(1+25%)-200=1050, a₁-800=250，∴a_n -800=250(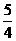)^n-1，a_n =250(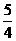)^n-1+800，令a_n≥4000，得(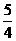)ⁿ≥16，解得n≥12,即至少要过12年才能达到目标。

有的应用题中的数列递推关系，a_n与a_n-1的差(或商)不是一个常数，但是所得的差f(n)本身构成一个等差或等比数列，这在一定程度上增加了递推的难度。

例2、某产品具有一定的时效性，在这个时效期内，由市场调查可知，在不作广告宣传且每件获利a元的前提下，可卖出b件。若作广告宣传，广告费为n千元时比广告费为(n-1)千元时多卖出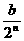件，(n∈N^*)。

(1)试写出销售量s与n的函数关系式；

(2)当a=10,b=4000时厂家应生产多少件这种产品，做几千元广告，才能获利最大？

分析：对于(1)中的函数关系，设广告费为n千元时的销量为s_n,则s_n-1表示广告费为(n-1)元时的销量，由题意，s_n--s_n-1=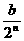，可知数列{s_n}不成等差也不成等比数列，但是两者的差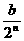构成等比数列，对于这类问题一般有以下两种方法求解：

解法一、直接列式：由题，s=b+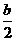++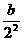+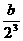…+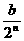=b(2-)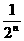

(广告费为1千元时，s=b+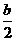；2千元时，s=b+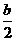+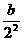；…n千元时s=b++++…+)

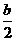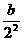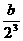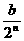解法二、(累差叠加法)设s₀表示广告费为0千元时的销售量，

由题：，相加得S_n-S₀=+++…+,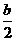

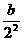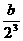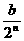即s=b+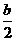++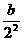+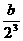…+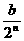=b(2-)。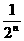

(2)b=4000时，s=4000(2-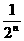),设获利为t,则有t=s·10-1000n=40000(2-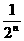)-1000n

欲使T_n最大，则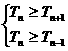：，得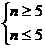，故n=5,此时s=7875。

即该厂家应生产7875件产品，做5千元的广告，能使获利最大。