
题目列表(包括答案和解析)
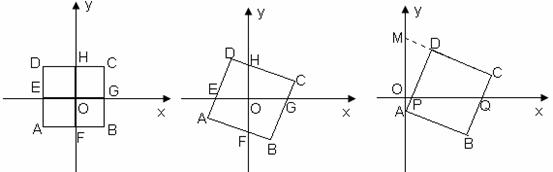
24.如图,在平面直角坐标系中,正方形ABCD的边DA、AB分别垂直于x轴、y轴,原点O在正方形ABCD的对称中心,正方形各边分别交坐标轴于E、F、G、H四点
(1)EG与FH有何数量关系,直接写出你的猜想为:
(2)将图①中的正方形ABCD绕原点O顺时针旋转角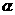 (
(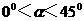 ),如图②。请问:你在(1)中猜想的结论还成立吗?说明理由。
),如图②。请问:你在(1)中猜想的结论还成立吗?说明理由。
(3)将图②中的正方形ABCD沿x轴向右平移,使原点O落在正方形ABCD的外部,点A落在y轴上,CD的延长线交y轴于点M,AD、BC分别交x轴于点P、Q,如图③。已知A点坐标为(0,-1),M点坐标为(0,4)。请你在直线BC上找出一点T,使T到AM的距离等于PQ的长,并求出直线OT的解析式。
23.“六·一”儿童节期间,某超市将销售价为每个30元的某种儿童玩具实行降价促销,在促销中发现,当每个玩具的销售价降低x元时,日销售量y(个)与x(元)之间满足关系式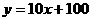 。已知超市购进这种玩具所需成本为每个10元。
。已知超市购进这种玩具所需成本为每个10元。
(1)用含x的代数式表示:降价后,每个玩具的实际销售价为 元,每个玩具的利润为 元;
(2)设降价后该玩具每日的销售利润为W元,求W与x之间的函数关系式;
(3)若规定每个玩具的降价不得超过10元,试问:当该玩具的日销售量最大时,每日的销售利润能否也最大?为什么?
22.(本小题满分8分)
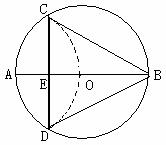
如图,斌斌要在一块圆形纸板中尽量不浪费地裁剪出一个等边三角形;他是这么做的:先画⊙O的直径AB,再将图形折叠,使A点与O点重合,折痕CD交AB于E。
(1)判断以A、D、O、C为顶点的四边形是什么四边形? (将结果直接写在横线上)
(2)求证:△CDB是等边三角形。
21.(本小题满分7分)
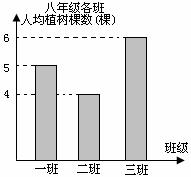
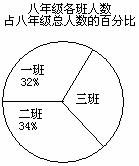
为“保护环境,绿化江河”,植树节这天,某中学八年级(一)、(二)、(三)班的学生积极参加植树活动。已知该校八年级共有3个班,且这三个班共有学生200人。根据右图所给信息解答:
(1)八年级(三)班共有多少学生?
(2)这三个班共植树多少课?
20.(本题共2个小题,其中第<1>小题3分,第<2>小题4分,满分7分)
(1)连续两次掷一枚均匀的骰子,则两次所掷骰子的点数和为8的概率是 (直接写出结果)。
(2)如图,广宇购物中心设立了一个可以自由转动的转盘,并规定:顾客购物20元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品。下表是活动进行中的一组统计数据。
|
转动转盘的次数n |
100 |
200 |
400 |
500 |
1000 |
|
落在“牙膏”的次数m |
58 |
58 |
121 |
149 |
300 |
落在“牙膏”的频率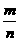 |
|
|
0.3025 |
|
|
①
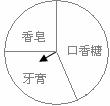 计算并完成上面的表格
计算并完成上面的表格
② 请估计,当n很大时,频率将会接近多少?
③ 假如你去转动该转盘一次,你获得牙膏的概率时多少?
19.(本小题满分7分)
解不等式组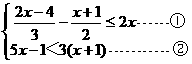 ,并把它的解集在数轴上表示出来。
,并把它的解集在数轴上表示出来。
18.(本小题满分7分)
计算: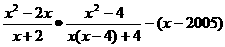
17.如图,右边①、②、③、④四个大正方形都是由四个边长为1的小正方形组成的,请你仔细观察,其中阴影部分面积最大的图形是 。(填序号)

① ② ③ ④
16.“五·一”节期间,某商场为吸引顾客,实行“买100送20,连环送”的活动,即顾客购物满100元,就可以获赠商场购物券20元,不足100元的部分不赠券,并且购物可以用现金,也可以用购物券。如果你有340元现金,在活动期间到该商场购物,最多可以获赠购物券累计为 元。
15.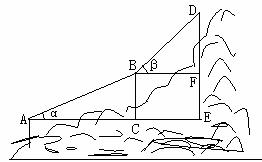 如图,已知登山缆车行驶路线与水平线间的夹角α=30°,β=45°。小勇乘缆车上山,从A到B,再从B到D均走了100米(即AB=BD=100米),则缆车垂直上升的高度DE为
米。(结果保留根号)
如图,已知登山缆车行驶路线与水平线间的夹角α=30°,β=45°。小勇乘缆车上山,从A到B,再从B到D均走了100米(即AB=BD=100米),则缆车垂直上升的高度DE为
米。(结果保留根号)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com