
题目列表(包括答案和解析)
4. 有N件产品,其中有M件次品,从中不放回地抽n 件产品,抽到的次品数的数学期望值是
A.
n
B. 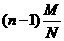 C.
C. 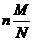 D.
D. 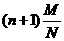 ( )
( )
3. 已知随机变量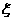 的分布列为
的分布列为
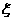 |
-1 |
0 |
1 |
|
P |
0.5 |
0.3 |
0.2 |
则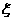 最可能出现的值是
( )
最可能出现的值是
( )
A. 0.5 B. -1 C. 0 D. 1
2. 某批量较大的产品的次品率为10%,从中任意连续取出4件,则其中恰好含有3件次品的概率是
A. 0.0001 B. 0.0036 C. 0.0486 D. 0.2916 ( )
1. 下列随机变量中,不是离散随机变量的是 ( )
A. 从10只编号的球 ( 0号到9号) 中任取一只,被取出的球的号码
B. 抛掷两个骰子,所得的最大点数
C. [0 , 10]区间内任一实数与它四舍五入取整后的整数的差值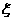
D. 一电信局在未来某日内接到的 电话呼叫次数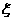
22.[本题满分共18分]
已知c>0,
设P:函数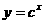 在R上单调递减;Q:不等式
在R上单调递减;Q:不等式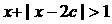 的解集为R;
的解集为R;
如果P和Q中有且仅有一个正确,试求c的取值范围.
解:
21.[本题满分共16分]
某货运公司今年初用98万元购进一批货车,这批货车第一年需各种费用12万元。从第二年开始,包括维修费在内,每年所需费用均比上一年增加4万元。该批货车每年运货的总收入为50万元。
(1)设该批货车运货n(n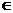 N)年后开始盈利(即总收入大于买车和其它所有费用之和),求:n.
N)年后开始盈利(即总收入大于买车和其它所有费用之和),求:n.
(2)(理)该货车运货若干年后,处理方案有两种:
① 到年平均盈利达到最大值时,以26万元的价格全部买出。
② 当盈利总额达到最大值时,以8万元的价格全部买出。问哪一种方案较为
合算?请说明理由。
(文)几年后年平均盈利达到最大值,并求出最大值。
解:
20.[本题满分共14分,(1)满分6分,(2)满分8分]
已知函数y =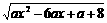 的定义域为R,
的定义域为R,
(1) 求实数a的取值范围;
(2) 当x变化时,若y的最小值为f(a),求f(a)的值域。
19.[本题满分共14分]
已知a>0且a≠1,解关于x的不等式1+log2(ax-1)≤log4(4-ax)
解:
18.[本题满分共12分]
已知集合A ={x|x2-(t2+t+1)x+t(t2+1)>0}}, B ={x|x=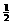 m2-m+
m2-m+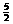 , 0≤m≤3},若AÇB=
, 0≤m≤3},若AÇB=
Φ,求实数t的取值范围.
解:
17.[本题满分共12分]
已知f(x)=(1+2x)m+(1+3x)n(n、mÎN)的展开式中x的系数为13,且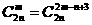 ,
,
(1)求m、n的值; (8分) (2)求展开式中含x2项的系数。 (4分)
解:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com