
题目列表(包括答案和解析)
例1:若点P(3m-2,5-2m)在第二象限,求m的取值范围
解:∵点P(3m-2,5-2m)在第二象限
 ∴
3m-2<0 解得:m<
∴
3m-2<0 解得:m<
5-2m>0
注:根据各象限内点的横纵坐标的特征列出两个不等式,组成不等式组即可求得。
例2:若A点坐标为(m,n),它关于原点的对称点为A1,而A1关于x轴的对称点为A2,且点A2的坐标为(3,-4),求m、n的值。
解:∵A点坐标为(m,n)
∴A点关于原点的对称点A1的坐标为(-m,-n),A1点关于x轴的对称点A2的坐标为(-m,n)
又∵点A2的坐标为(3,-4)
 ∴ -m=3 即:m=-3
∴ -m=3 即:m=-3
n=-4 n=-4
注:本题是按题意中的对称关系顺次由点A的坐标推得点A2的坐标。由于点的轴对称和中心对称关系是相互的,所以本题也可由点A2的坐标逆方向求点A的坐标,即:A2(3,-4)→A1(3,4)→A(-3,-4)→m=-3,n=-4
例3:已知点P(a,a-b)在第四象限,求:(1)Q(-a,b)所在象限。(2)若a=b,则P点和Q点在什么位置?
解:(1)∵P(a,a-b)在第四象限
∴a>0,且a-b<0
 ∴
b>a>0
∴
b>a>0
-a<0
则:Q(-a,b)在第二象限
(2)当a=b时,P、Q两点坐标可分别表示为
P(a,0) Q(-a,a)
又∵a>0
∴P点在x轴正半轴上,Q点在第二象限角平分线上(原点除外)。
注:(1)因为P点在第四象限,横坐标a为正值,纵坐标a-b应为负值,所以b必大于a,也为正数;(2)当点的横、纵坐标相同时,该点在一、三象限角平分线上。而点的横、纵坐标互为相反数时,点必在二、四象限角平分线上。本例有前提P在第四象限a>0,所以Q只能在第二象限角平分线上,且原点要除外。
例4:求下列各函数的自变量取值范围
(1)
(2)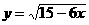
(3)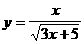
(4)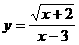
(5)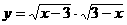
(6)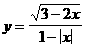
(7)
解:(1)∵不论x取什么值,原函数都有意义
∴x为全体实数
(2)要使函数有意义,必须使15-6x≥0
∴x≤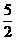
(3)要使函数有意义,只须3x+5>0,∴x>-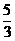
(4)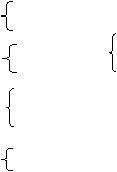 要使函数有意义,必须使 x+2≥0
∴x≥-2且x≠3
要使函数有意义,必须使 x+2≥0
∴x≥-2且x≠3
x-3≠0
(5)要使函数有意义,必须使 x-3≥0 即 x≥3 ∴x=3
3-x≥0 x≤3
(6)要使函数有意义,必须使 3-2x≥0 ∴x≤ 且x≠±1
且x≠±1
1-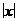 ≠0
≠0
(7)要使函数有意义,必须使 x≠0 ∴x≠0,x≠-1且x≠3
x2-2x-3≠0
例5:如图,锐角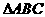 中,BC=10,高AD=6,EFGH是它的内接矩形,设EF为x,EH为y.求y与x的函数关系式
中,BC=10,高AD=6,EFGH是它的内接矩形,设EF为x,EH为y.求y与x的函数关系式
分析:①学会在图中标注数据
②EFGH是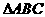 的内接矩形,本身隐含着EH∥BC这一条件
的内接矩形,本身隐含着EH∥BC这一条件
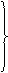
 ③EH∥BC提供
③EH∥BC提供 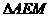 ∽
∽
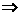
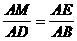
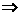

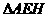 ∽
∽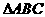
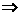
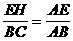
即: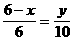 ,变形即得:
,变形即得: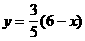
④x是矩形一边EF的长度,因此0<x<6,这里x≠0且x≠6
因为x=0或x=6时矩形都不存在,也就失去了该题的实际意义了。
解:∵EFGH为矩形

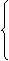 ∴EH∥BC
∴EH∥BC 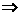
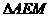 ∽
∽
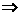
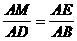
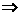
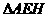 ∽
∽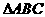
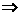
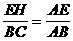
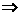

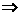
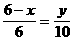
∴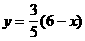 (0<x<6)
(0<x<6)
注:对根据实际问题得到的函数关系,它的自变量取值不仅要使函数解析式有意义,而且还要使实际问题有意义,应根据实际问题的限制,确定自变量的取值范围。

例6:求 ,当x=12时的函数值
,当x=12时的函数值
分析:实质上是当x=12时,求代数式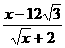 的值。
的值。
解:当x=12时

=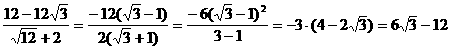
例7:当x为何值时, 与y=1-x的函数值相等
与y=1-x的函数值相等
分析:此题即x为何值时 成立
成立
解:当 时
时
即:x2+x=0 ∴x1=-1,x2=0
经检验:x1=-1,x2=0都是原方程的根。
∴当x=-1或x=0时,两函数值相等。
6、 关于函数图象的意义,要注意到是“把自变量x与函数y的每对对应值分别作为点的横坐标与纵坐标。”
5、 对于函数的三种常用的表示方法,应该有这样的认识:给出一种函数关系,根据需要,有时可以写出它的解析表达式,有时可以列出函数与其自变量的对应数值表,有时也可以画出它的图象;反过来,也可以用一个解析式,或一个反映两个变量的对应关系的数值表,或一个图象,来表示一个函数关系。
4、 关于函数值的问题,可以和求代数式的值的问题联系起来,注意运算的熟练与准确程度。
3、 关于函数自变量的取值范围问题,主要包含两个方面:一是自变量的取值使函数解析式有意义,这是常用的一个方面,也是以前学过的知识;二是自变量的取值使实际问题有意义,这一方面虽然用的不多,但需要对实际问题作具体分析,有一定难度。
2、 对于函数的意义,在初中阶段主要应领会两点:一是有两个变量,二是一个变量的数值随着另一个变量的数值变化而变化。
1、 平面直角坐标系是以数轴为基础的,坐标平面内的点的坐标也是利用数轴上点的坐标来定义的。有关直角坐标系的概念比较多,学习时应紧密结合图形,不能死记硬背定义,看到一个概念,脑子里要能马上反映出相关的图形。如对“象限”的理解,关键在于结合直角坐标系,能指出各个象限的位置,进而明确坐标轴上的点不属于任何一个象限的真正含义。
4、 函数的三种表示方法及用描点法画函数图像。
3、 对函数概念的理解和自变量取值范围的确定。
2、 懂得建立了平面直角坐标系,就使平面上的点与一对有序实数之间建立起一一对应关系,建立数与形之间的联系,初步了解数形结合思想。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com