
题目列表(包括答案和解析)
6.函数 的值域是_____
的值域是_____ _____.
_____.
5.已知 ,
,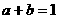 ,则
,则 +
+ 的范围是__
的范围是__ __.
__.
4.设等差数列 的公差
的公差 ,且
,且 ,则
,则 的值为(C)
的值为(C)
A. 85 B. 72.5 C. 60 D. 52.5
3.已知x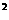 +4y
+4y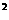 =4x,则x+y的范围是_____
=4x,则x+y的范围是_____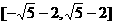 ______.
______.
2.已知数列 中,
中, a
a =-1,则数列通项
=-1,则数列通项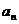 =_____
=_____ ____.
____.
1.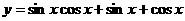 的最大值是__
的最大值是__ +
+ ___.
___.
例1.(1)已知: ,求
,求 .
.
(2)设实数 、
、 满足
满足 ,则
,则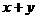 的取值范围是_________.
的取值范围是_________.
(3)方程 的解集是______________.
的解集是______________.
解:(1) ;
;
(2)设 ,则
,则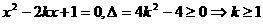 或
或 ;
;
(3)令 =
= ,可得原方程的解集为
,可得原方程的解集为 .
.
例2.(1)函数 的值域是_____________.
的值域是_____________.
(2)已知:数列 的
的 ,前
,前 项和为
项和为 ,
, .求
.求 的通项公式.
的通项公式.
解:(1)令 ,
, ,则
,则
 , ∴
, ∴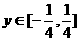 .
.
(2)由 ,知
,知 ,
,
∴ ,即
,即
∴ ,令
,令 ,则
,则
∵ ,
,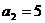 ,∴
,∴ ,
, ,即
,即 .
.
两边除以 得:
得: ,令
,令 ,则有
,则有 ,
,
∴ ,代入
,代入 得:
得:  .
.
例3.实数x、y满足4x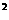 -5xy+4y
-5xy+4y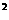 =5 ( ①式) ,设S=x
=5 ( ①式) ,设S=x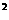 +y
+y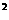 ,求
,求 +
+ 的值.(93年全国高中数学联赛题)
的值.(93年全国高中数学联赛题)
方法1:设 代入①式得: 4S-5S·sin
代入①式得: 4S-5S·sin cos
cos =5
=5
解得 S= ;
;
∵ -1≤sin2α≤1 ∴ 3≤8-5sin2α≤13 ∴  ≤
≤ ≤
≤
∴  +
+ =
= +
+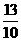 =
= =
=
方法2:由S=x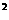 +y
+y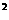 ,设x
,设x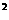 =
= +t,y
+t,y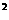 =
= -t,t∈[-
-t,t∈[- ,
, ],
],
则 代入①式得:4S±5
代入①式得:4S±5 =5,
=5,
移项平方整理得 100t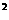 +39S
+39S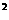 -160S+100=0 .
-160S+100=0 .
∴
39S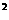 -160S+100≤0 解得:
-160S+100≤0 解得: ≤S≤
≤S≤
∴  +
+ =
= +
+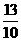 =
= =
=
方法3:(和差换元法)设x=a+b,y=a-b,代入①式整理得3a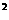 +13b
+13b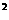 =5 ,求得a
=5 ,求得a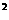 ∈[0,
∈[0, ],所以S=(a-b)
],所以S=(a-b) +(a+b)
+(a+b) =2(a
=2(a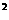 +b
+b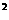 )=
)= +
+ a
a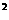 ∈[
∈[ ,
, ],再求
],再求 +
+ 的值.
的值.
解数学题时,把某个式子看成一个整体,用一个变量去代替它,从而使问题得到简化,
这叫换元法.
换元的方法有:局部换元、三角换元、均值换元等.
22.已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的一个顶点,BC过椭圆中心O,且 ,|BC|=2|AC|.
,|BC|=2|AC|.
(1)求椭圆方程;
(2)如果椭圆上两点P、Q,使 PCQ的平分线垂直AO,是否总存在实数
PCQ的平分线垂直AO,是否总存在实数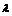 ,使
,使 ?请给出说明。
?请给出说明。
21.已知 、
、 、
、 ,
,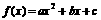 .
.
(1)若 ,
, 在[-1,1]上的最大值为2,最小值为
在[-1,1]上的最大值为2,最小值为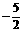 ,求证:
,求证: 且
且 ;
;
(2)若a>0,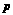 、
、 满足
满足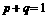 ,且对任意
,且对任意 、
、 R,均有
R,均有 ≥
≥ ,求证:
,求证:
0≤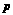 ≤1.
≤1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com