10.已知二次函数y＝f(x)在x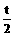＝+1处取得最小值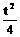－(t＞0),f(1)＝0(95上海) ⑴求y＝f(x)的表达式； ⑵若任意实数x都满足等式f(x)g(x)+a_nx+b_n＝xⁿ⁺¹(其中g(x)为多项式，n∈N),试用t表示a_n和b_n； ⑶设圆C_n的方程为：(x－a_n)²+(y－b_n)²＝r_n²,圆C_n与圆C_n+1外切(n＝1,2,3…)，{r_n}是各项都为正数的等比数列，记S_n为前n个圆的面积之和，求r_n和S_n.

9.　　 某地为促进淡水鱼养殖业的发展，将价格控制在适当范围内，决定对淡水鱼养殖提供政府补贴，设淡水鱼的市场价格为x元/千克，政府补贴为t元/千克，根据市场调查，当8≤x≤14时，淡水鱼的市场日供应量P千克与市场日需求量Q千克近似地满足关系: P＝1000(x+t－8)　 (x≥8，t≥0) Q＝500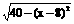 (8≤x≤14) 当P＝Q时的市场价格称为市场平衡价格. ①将市场平衡价格表示为政府补贴的函数，并求出函数的定义域； ②为使市场平衡价格不高于每千克10元，政府补贴至少为每千克多少元?(95(25)12分)

8.　　 已知函数f(x)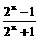＝(91三南) ⑴证明：f(x)在(－∞,+∞)上是增函数； ⑵证明：对不小于3的自然数n都有f(n)＞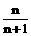

7. 根据函数单调性的定义，证明函数f(x)＝－x³+1在R上是减函数.(91(24)10分)

6. 设f(x)＝lg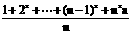，其中a是实数，n是任意给定的自然数，且n≥2. ①如果f(x)当x∈(－∞，1]时有意义，求a的取值范围； ②如果a∈(0，1]，证明2f(x)＜f(2x)当x≠0时成立.(90(24)10分)

5. 设f(x)是定义在R上以2为周期的函数，对k∈Z，用I_k表示区间(2k－1，2k+1]，已知当x∈I₀时，f(x)＝x².(89(24)10分) ①求f(x)在I_k上的解析表达式； ②对自然数k，求集合M_k＝{a|使方程f(x)＝ax在I_k上有两个不相等的实根}

4. 已知a＞0且a≠1，试求使方程log_a(x－ak)＝log_a2(x²－a²)有解的k的取值范围.(89(22)12分)

3. 给定实数a，a≠0且a≠1，设函数y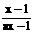＝(x∈R且x≠)，证明: ①经过这个函数图象上任意两个不同点的直线不平行于x轴； ②这个函数的图象关于直线y＝x成轴对称图形.(88(24)12分)

2. 已知集合A和集合B各含有12个元素，A∩B含有4个元素，试求同时满足下面两个条件的集合C的个数:①CÍA∪B，且C中含有3个元素，②C∩A≠φ(φ表示空集)(86(20)10分)

1. 设a，b是两个实数，A＝{(x，y)|x＝n，y＝na+b，n是整数}，B＝{(x，y)|x＝m，y＝3m²+15，m是整数}，C＝{(x，y)|x²+y²≤144}是xoy平面内的集合，讨论是否存在a和b使得①A∩B≠φ，②(a，b)∈C同时成立.(85(17)12分)