
题目列表(包括答案和解析)
线线、线面、面面关系贯穿于立体几何始终,距离问题便是依托于这三种关系及其转化的一种重要问题。
例1. (’89全国高考)如图,已知圆柱的底面半径是3,高为4,A、B两点分别在两底面的圆周上,并且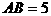 ,求直线AB与轴
,求直线AB与轴 之间的距离。
之间的距离。
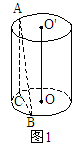
分析:如图1,过A作AC垂直于底面,垂足为C,连结BC,则 平面ABC
平面ABC
显然两直线 与AB的距离,即可转化为直线
与AB的距离,即可转化为直线 与平面ABC的距离,进而转化为O到平面ABC的距离,易得,所求距离
与平面ABC的距离,进而转化为O到平面ABC的距离,易得,所求距离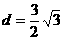 。
。
说明:两条异面直线的距离,线面距离,点面距离。面面距离,既相互联系,又可相互转化。距离转化策略,正是解决此类问题的上策。
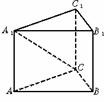
8.(2003年上海春季高考题)已知三棱柱ABC-A1B1C1,在某个空间直角坐标系中,
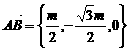 ,
,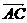 ={m,0,0},
={m,0,0},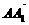 ={0,0,n},其中m、n>0.
={0,0,n},其中m、n>0.
(1)证明:三棱柱ABC-A1B1C1是正三棱柱;
(2)若m=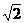 n,求直线CA1与平面A1ABB1所成角的大小.
n,求直线CA1与平面A1ABB1所成角的大小.
高考能力测试步步高数学基础训练34答案
7.已知空间三点A(1,2,3),B(2,-1,5),C(3,2,-5).
 试求:(1)△ABC的面积;
试求:(1)△ABC的面积;
(2)△ABC的AB边上的高.
6.已知△ABC中,A(2,-5,3),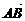 =(4,1,2),
=(4,1,2),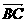 =(3,-2,5),求其余顶点与向量
=(3,-2,5),求其余顶点与向量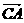 及∠A.
及∠A.
5.直二面角α-l-β,线段AB,A∈α,B∈β,AB与α所成的角为30°,则AB与β所成角的取值范围是_________.
4.在棱长为1的正方体ABCD-A1B1C1D1中,E是棱BB1的中点,P是截面ABC1D1上的一动点,则A1P+PE的最小值为_________.
3.将锐角为60°,边长为a的菱形ABCD沿较短的对角线折成60°的二面角,则AC与BD的距离为
A.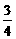 a B.
a B.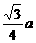 C.
C.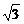 a
D.
a
D.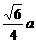
2.α-a-β的平面角是锐角θ,α内一点A到棱a的距离为4,点A到面β的距离为3,则tanθ的值等于
A.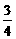 B.
B.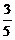 C.
C.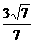 D.
D.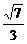
1.已知点A、B、C、D的坐标分别为(-1,0,1),(0,0,1),(2,2,2)(0,0,3),则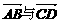 所成的角为
所成的角为
A.arccos(-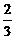 ) B.-arccos(-
) B.-arccos(-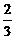 )
)
C.arccos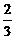 D.-arccos
D.-arccos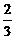
8.在棱长为a的正四面体ABCD中,M、E分别是棱BD、BC的中点,N是BE的中点,连结DE、MN,求直线DE与平面AMN间的距离.
基础训练34(B) 夹角与距离的计算
●训练指要
掌握空间有关角和距离的确定方法、范围,熟练地计算空间的角和距离.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com