
题目列表(包括答案和解析)
7.椭圆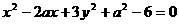 的一个焦点在直线
的一个焦点在直线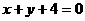 上,则
上,则 ( C )
( C )
A.2 B.-6 C. -2或-6 D. 2或6
6.设 和
和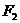 为双曲线
为双曲线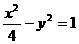 的两个焦点,点
的两个焦点,点 在双曲线上且满足
在双曲线上且满足 ,则△
,则△ 的面积是___1___.
的面积是___1___.
5.函数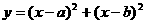 (
( 、
、 为常数)的最小值为( B
)
为常数)的最小值为( B
)
A.8
B. C.
C. D.最小值不存在
D.最小值不存在
4.已知方程 的两根
的两根 、
、 ,且点
,且点 (
( ,
, )在圆x
)在圆x +y
+y =4上,则实数
=4上,则实数 =___
=___ __.
__.
3.函数 的单调递增区间是( D
)
的单调递增区间是( D
)
A.  B.
B.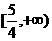 C.
C. D.
D.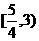
2.方程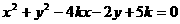 表示圆的充要条件是___
表示圆的充要条件是___ ____.
____.
1.在正项等比数列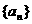 中,
中,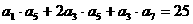 ,则
,则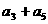 =___5___.
=___5___.
例1.已知长方体的全面积为11,其12条棱的长度之和为24,则这个长方体的一条对角线长为_____.
A. 2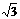 B.
B.  C. 5
D. 6
C. 5
D. 6
解:设长方体长宽高分别为 ,由已知“长方体的全面积为11,其12条棱的长度之和为24”而得:
,由已知“长方体的全面积为11,其12条棱的长度之和为24”而得: .
.
长方体所求对角线长为: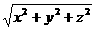 =
=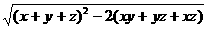 =
=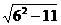 =5,所以选B.
=5,所以选B.
例2. 设方程 的两实根为
的两实根为 、
、 ,若(
,若(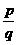 )
) +(
+( )
) ≤7成立,求实数
≤7成立,求实数 的取值范围.
的取值范围.
解:方程 的两实根为
的两实根为 、
、 ,由韦达定理得:
,由韦达定理得: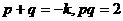 ,
,
(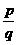 )
) +(
+( )
) =
=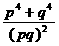 =
=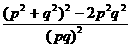 =
=
= ≤7, 解得
≤7, 解得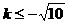 或
或 .
.
又 ∵ 、
、 为方程
为方程 的两实根, ∴
的两实根, ∴ 
即 或
或 ,
,
综上可得, 的取值范围是:-
的取值范围是:- 或
或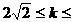
 .
.
例3.设二次函数 ,给定
,给定 、
、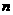
 ,且满足
,且满足
 ,
,
(1)解不等式 ;
;
(2)是否存在一个实数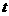 ,使当
,使当 时,
时, ?若不存在,说出理由;若存在,指出
?若不存在,说出理由;若存在,指出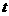 的取值范围.
的取值范围.
解:(1)由已知得,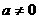 且
且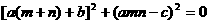 ,
,
∴ 即
即 、
、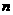 是方程
是方程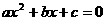 的两根,且
的两根,且 ,所以,
,所以,
当 时,
时, 的解集为
的解集为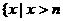 或
或 ;
;
当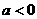 时,
时,  的解集为
的解集为 ,
,
(2)当 时,
时, 的解集为
的解集为 ,
,
若 ,则
,则 ,即
,即 时,
时, ;
;
 若
若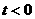 ,则
,则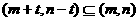 ,不满足对所有的
,不满足对所有的 ,
, .当
.当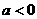 时,
时, 的解集为
的解集为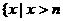 或
或 ,不存在
,不存在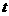 使得
使得
时, 成立.综上可得,当
成立.综上可得,当 时,存在
时,存在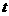 满足
满足 时,
时, ,此时
,此时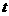 的取值范围为
的取值范围为 ;当
;当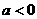 时不存在
时不存在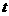 使得
使得 时,
时, 成立.
成立.
配方法主要适用于:已知或者未知中含有二次方程、二次不等式、二次函数、二次代数式的讨论与求解,或者缺xy项的二次曲线的平移变换等问题.常见配方形式,如:
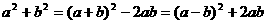 ;
;
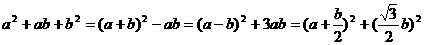 ;
;
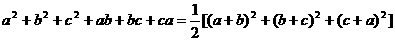 .
.
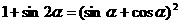 ;
;
 ;…… 等等.
;…… 等等.
22. (13分)
已知椭圆 的离心率是
的离心率是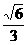 ,F是其左焦点,若直线
,F是其左焦点,若直线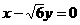 与椭圆交于AB两点,且
与椭圆交于AB两点,且 ,求该椭圆的方程。
,求该椭圆的方程。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com