

题目列表(包括答案和解析)
2、主题理论。教学过程:学生是能动的决定因素,教就是要为学服务,把学放在主体位置,把更多时间给学生,发挥学习的能动性,注意针对性。复习时,应从学生实际出发,针对知识缺陷,精选习题,让学生练习。练习时采用这样的方法“延时讲解--分析思路--解题小结”,延时讲解是让学生看过题目后,自己进行分析思考,主要是要提高学生的审题能力,通过审题收集信息,加工信息,熟悉题目并深入到题目内部去思考,就会找到解题的入口,也会在解题的全过程中,不忽视任何一个细节,这是把学生摆在主体位置的一个重要方面。现代心理学认为,学生的解题活动必须置于教师的合理控制之下,才会收到较好的效果。分析思路就是一个控制手段,最后解题完毕进行小结,指出本题所运用到的某一个数学思想方法或技能的道理,练习解题,要使学生达到“三化”的要求:通过练习使学生对基本知识能消化,对基本方法的运用达到优化,对基本方法的掌握能强化。
教师在第一轮复习的基础上,进入第二轮从本质上讲,是将学过的知识和已具备的基本技能和方法运用于解决问题的一种复习。因此,复习运用好下面两个理论来指导,会收到事半功倍的效果。
1、整体原理。系统论中一个原理:任何系统内部各部分都是互相作用,互相联系的,任何系统都与外部发生联系,总体功能大于部分功能,部分离开整体就失去其功能。如在解专题复习中,抓住数形结合这个整体思想,把各部分知识联系起来,即在平面建立坐标系统后,曲线应用方程表示直线用一次方程来表示,圆锥曲线用二次方程来表示,运用整体原理,就是这么几句话就把一本书的内容总结出来,不仅容易记住基本知识,又学会数形结合的数学解题思想。又如立体几何专题部分的复习,只要抓住“点、线、面”三者间的位置关系的整体思想,从平面到空间来构建知识平台。从而达到这本几何读薄。
22.(本小题满分13分)
(理)若{an}是正项递增的等差数列,n∈N,k≥2,k∈N,求证:
(Ⅰ)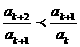 ;
;
(Ⅱ)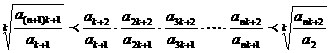 ;
;
(文)已知等比数列{xn}的各项为不等于1的正数,数列{yn}满足yn·logxna=2(a>0且
a≠1),设y3=18,y6=12.
(Ⅰ)求数列{yn}的前多少项和最大,最大值为多少?
(Ⅱ)试判断是否存在自然数M,使当n>M时,xn>1恒成立?若存在,求出相应的M,若不存在,请说明理由;
(Ⅲ)令an=logxnxn+1(n>13,n∈N),试判断数列{an}的增减性?
21.(本小题满分12分)
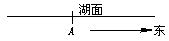 (理)在东西方向直线延伸的湖岸上有一港口A,一艘机艇以40 km/h的速度从A港出发,30分钟后因故障而停在湖里,已知机艇出发后,先按直线前进,以后又改成正北,但不知 最初的方向和何时改变的方向,如果去营救,用图示表示营救区域(提示:满足不等式y≥ax+b的点(x,y)不在y=ax+b的下方).
(理)在东西方向直线延伸的湖岸上有一港口A,一艘机艇以40 km/h的速度从A港出发,30分钟后因故障而停在湖里,已知机艇出发后,先按直线前进,以后又改成正北,但不知 最初的方向和何时改变的方向,如果去营救,用图示表示营救区域(提示:满足不等式y≥ax+b的点(x,y)不在y=ax+b的下方).
(文)国贸城有一个个体户,2001年一月初向银行贷款10万元作开店资金,每月底获得的利润是该月初投入资金的20%,每月底所缴的房租和所得税为该月所得金额(含利润)的10%,每月生活费和其他开支为3000元,余款作为资金全部投入再营业,如此继续,问到2001年年底,这一个体户有现款多少元?(1.0812≈2.5)
20.(本小题满分13分)
已知抛物线C:y=-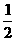 x2+6,点P(2,4),A、B在抛物线上,且直线PA、PB的倾斜角互补;
x2+6,点P(2,4),A、B在抛物线上,且直线PA、PB的倾斜角互补;
(Ⅰ)证明:直线AB的斜率为定值;
(Ⅱ)当直线AB在y轴上的截距为正数时,求△PAB的面积S的最大值及此时直线AB的方程.
19.(本小题满分12分)
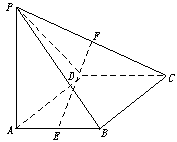
在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点,
(Ⅰ)求证:CD⊥PD;
(Ⅱ)求证:EF∥平面PAD;
(Ⅲ)当平面PCD与平面ABCD成多大角时,直线EF⊥平面PCD.
18.(本小题满分12分)
已知复数z满足(z+1)(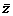 +1)=|z2|,且
+1)=|z2|,且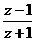 是纯虚数;
是纯虚数;
(Ⅰ)求z;
 (Ⅱ)求argz.
(Ⅱ)求argz.
17.(本小题满分12分)
已知集合A={x|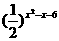 <1},B={x|log4(x+a)<1},若A∩B=
<1},B={x|log4(x+a)<1},若A∩B=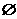 ,求实数a的取值范围.
,求实数a的取值范围.
16.在△ABC中A>B,下列不等式中正确的是
①sinA>sinB;②cosA<cosB;③sin2A>sin2B;④cos2A<cos2B
其中正确的序号为______________.
15.(理)已知直线l的参数方程为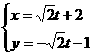 (t为参数),若以原点为极点,x轴的正半轴为极轴的极坐标系中,点P的极坐标为(-2,π),则点P到直线l的距离为______________.
(t为参数),若以原点为极点,x轴的正半轴为极轴的极坐标系中,点P的极坐标为(-2,π),则点P到直线l的距离为______________.
(文)函数y=sinx-|sinx|的最小值为______________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com