

题目列表(包括答案和解析)
19. (本小题满分12分)
(1) 由条件得:a +2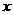 b
=–
b
=–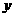 a +
a + 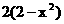 b,
b,
∴ 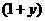 a +
a +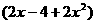 b = 0 ,
b = 0 ,
∵向量 a与b 不共线, ∴ 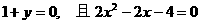 ,
,
解得 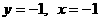 或
或 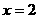 .
.
(2) ∵ a·b = cos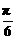 sin
sin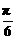 + sin(–
+ sin(–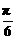 )cos
)cos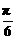 = 0, ∴a⊥b .
= 0, ∴a⊥b .
又∵c⊥d , ∴c·d = 0.
∵由条件知: |a | = 1, | b | = 1, a·b = 0,
∴ c·d = (a +2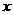 b)·[–
b)·[–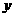 a +
a + 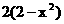 b]
b]
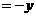 a 2
a 2 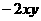 a·b+
a·b+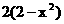 a·b
a·b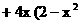 )b 2
)b 2 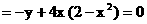 .
.
∴ 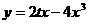 , 即
, 即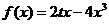 .
.
18. (本小题满分12分)
(1)∵ 这辆汽车在第一、二个交通岗均未遇到红灯,而第三个交通岗遇到红灯
∴ 概率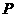 = (1 –
= (1 –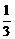 )(1 –
)(1 –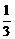 )
)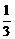 =
= 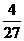 ;
;
(2)(理)∵
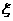 ∽
∽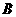 ( 8,
( 8, 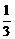 ),
),
∴ 期望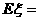 8´
8´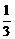 =
=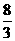 , 方差
, 方差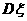 = 8´
= 8´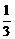 ´( 1 –
´( 1 –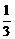 ) =
) = 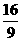 .
.
(文)概率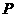 =
= 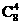 ´(
´(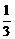 )4´ (1–
)4´ (1–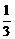 )2 =
)2 = 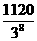 .
. 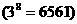
17. (本小题满分12分)
∵ 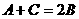 ,∴
,∴ 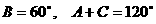 .
.
由 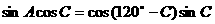 , 得
, 得
即 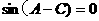
又 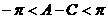 , ∴
, ∴ 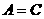 , △
, △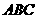 为等边三角形.
为等边三角形.
13.  /真 14.
/真 14. 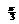 15. 0.99 16. 126, 24789
15. 0.99 16. 126, 24789
23. (附加题, 本题满分6分, 但全卷总分不超过150分)
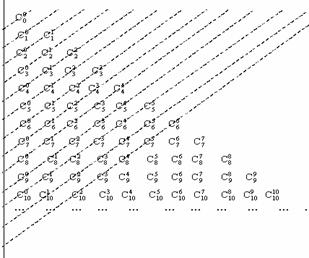
把“杨辉三角形”向左对齐如图所示,
分别按图中虚线,由上至下把划到的数相加,
写在虚线左下端点(左边竖线的左侧)处,
把这些和由上至下排列得一个数列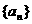 .
.
(1) 观察数列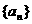 ,写出一个你能发
,写出一个你能发
现的递推公式(不必证明);
(2) 设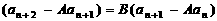 ,
,
求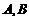 的值, 并求
的值, 并求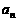 .
.
高考科目教学质量第一次检测
数学参考评分标准 (文理合卷)
22. (本小题满分14分)
定义在定义域D内的函数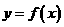 ,若对任意的
,若对任意的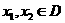 都有
都有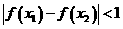 ,则称函数
,则称函数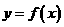 为“西湖函数”,否则称“非西湖函数”.函数
为“西湖函数”,否则称“非西湖函数”.函数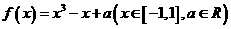 是否为“西湖函数”?如果是,请给出证明;如果不是,请说明理由.
是否为“西湖函数”?如果是,请给出证明;如果不是,请说明理由.
21. (本小题满分12分)
已知数列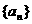 ,其中
,其中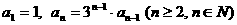 , 数列
, 数列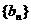 的前
的前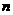 项的和
项的和
 .
.
(1) 求数列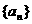 的通项公式;
的通项公式;
(2) 求数列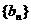 的通项公式;
的通项公式;
(3) (理科做文科不做) 求数列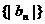 的前n项和
的前n项和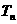 .
.
20. (本小题满分12分)
已知一物体做圆周运动, 出发后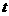 分钟内走过的路程
分钟内走过的路程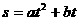 , 最初用5分钟走完第一圈, 接下去用3分钟走完第二圈.
, 最初用5分钟走完第一圈, 接下去用3分钟走完第二圈.
(1) 试问该物体走完第三圈用了多长时间? (结果可用无理数表示)
(2) (理科做文科不做) 试问从第几圈开始, 走完一圈的时间不超过1分钟?
19. (本小题满分12分)
已知平面向量 a与b 不共线,若存在非零实数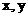 , 使得 c = a +2
, 使得 c = a +2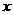 b ,
b ,
d =–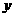 a +
a + 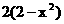 b .
b .
(1) 当c= d时,求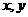 的值;
的值;
(2) 若a = (cos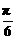 , sin(–
, sin(–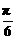 )), b = (sin
)), b = (sin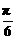 , cos
, cos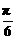 ),且c⊥d , 试求函数
),且c⊥d , 试求函数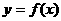 的表达式.
的表达式.
18. (本小题满分12分)
从汽车东站驾车至汽车西站的途中要经过8个交通岗,假设某辆汽车在各交通岗遇到红灯的事件是独立的,并且概率都是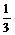 .
.
(1)求这辆汽车首次遇到红灯前,已经过了两个交通岗的概率;
(2)(理)这辆汽车在途中遇到红灯数ξ的期望与方差.
(文)这辆汽车在途中恰好遇到4次红灯的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com