

题目列表(包括答案和解析)
6. 已知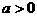 ,函数
,函数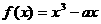 在
在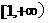 上是单调增函数,则a的最大值是( )
上是单调增函数,则a的最大值是( )
A. 3 B. 2 C. 1 D. 0
5. 设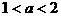 ,
,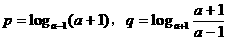 ,则
,则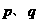 的大小关系是( )
的大小关系是( )
A. 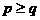 B.
B.
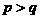 C.
C.
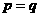 D.
D.
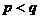
4. 如图是正方体的平面展开图,在这个正方体中
(1)BM与ED平行 (2)CN与BE是异面直线
(3)CN与BM成 (4)DN与BN垂直
(4)DN与BN垂直
以上四个命题中,正确命题的序号是( )
A. (1)(2)(3) B. (2)(4)
C. (3)(4) D. (2)(3)(4)
3. 已知等差数列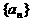 满足
满足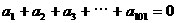 ,则有( )
,则有( )
A.  B.
B.
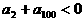
C. 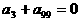 D.
D.
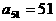
2. 已知复数Z,若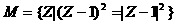 ,则M是( )
,则M是( )
A. M={虚数} B. M={实数}
C. {实数}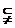 M
M 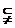 {复数} D.
M={复数}
{复数} D.
M={复数}
1. 已知映射: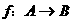 ,其中集合A={
,其中集合A={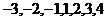 },集合B中的元素都是A中元素在映射f下的象,且对任意的
},集合B中的元素都是A中元素在映射f下的象,且对任意的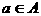 在B中和它对应的元素是| a |,则集合B中元素的个数是( )
在B中和它对应的元素是| a |,则集合B中元素的个数是( )
A. 4 B. 5 C. 6 D. 7
22.(本小题满分14分)
已知f(x)在(-1,1)上有定义,f(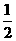 )=-1,且满足x,y∈(-1,1)有f(x)+f(y)=f(
)=-1,且满足x,y∈(-1,1)有f(x)+f(y)=f(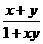 )
)
(Ⅰ)证明:f(x)在(-1,1)上为奇函数;
(Ⅱ)对数列x1=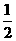 ,xn+1=
,xn+1=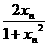 ,求f(xn);
,求f(xn);
(Ⅲ)求证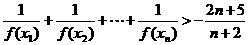
21.(本小题满分12分)
把长240cm,宽90cm的矩形铁皮的四角切去相等的正方形,然后折成一个无盖的长方
体的盒子,角上切去的正方形的边长为多少时,盒子的容积最大. 最大容积是多少?
19.(本小题满分12分)
 (甲)如图,正三棱柱
(甲)如图,正三棱柱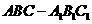 的底面边长为
的底面边长为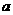 ,点
,点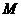 在边
在边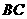 上,
上,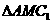 是以点M为直角顶点的等腰直角三角形.
是以点M为直角顶点的等腰直角三角形.
(Ⅰ) 求证点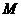 为边
为边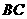 的中点;
的中点;
(Ⅱ) 求点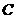 到平面
到平面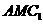 的距离;
的距离;
(Ⅲ) 求二面角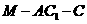 的大小.
的大小.
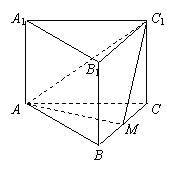
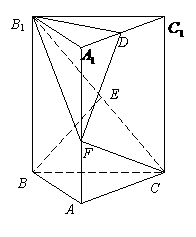 (乙) 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=
(乙) 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=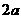 ,BB1=
,BB1=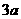 ,D为A1C1的中点,E为B1C的中点,
,D为A1C1的中点,E为B1C的中点,
(Ⅰ)求直线BE与A1C所成的角;
(Ⅱ)在线段AA1上是否存在点F,使CF⊥平面B1DF,若存在,求出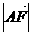 ;若不存在,说明理由.
;若不存在,说明理由.
 20.(本小题满分12分)
20.(本小题满分12分)
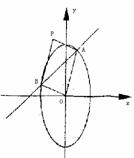
直线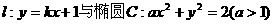 交于A、B
交于A、B
两点,以OA、OB为邻边作平行四边形OAPB(O为坐标原点).
(Ⅰ)若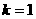 ,且四边形OAPB为矩形,求a的值;
,且四边形OAPB为矩形,求a的值;
(Ⅱ)若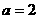 ,当k变化时(k∈R),求点P的轨迹方程.
,当k变化时(k∈R),求点P的轨迹方程.
18.(本题满分12分)
设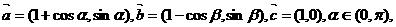
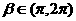 ,
,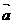 与
与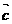 的夹角
的夹角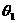 ,
,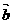 与
与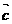 的夹角为
的夹角为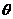 2,且
2,且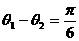 ,求
,求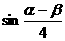 的值。
的值。
注意:考生在(19甲)、(19乙)两题中选一题作答,如果两题都答,只以(19甲)计分。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com