

题目列表(包括答案和解析)
15. 16. .
13. 14. .
16.函数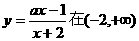 上是增函数,则实数a的取值范围是
.
上是增函数,则实数a的取值范围是
.

 试卷Ⅱ
试卷Ⅱ
15.已知集合A={x|2≤x≤π},定义在A上的函数y=logax (a>1)的最大值比最小值大1,则a的值等于 .
14.已知x, y 满足x2+2x+y2=0, 则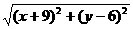 的最大值是
.
的最大值是
.
13.等比数列{an}的前n项和为Sn,若S3=2, S6=6.求a10+a11+a12= .
(1).若集合M={y|y=-2-x},P={y|y=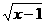 },则M∩P= ( )
},则M∩P= ( )
(A).{y|y<0} (B).{y|y≥1} (C).{y|y≥0} (D).
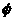
(2).下列函数中,既是偶函数,又在(0,π)内单调递增的函数是 ( )
(A).y=tan|x| (B).y=cos(-x)
(C).y=sin(x-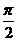 ) (D).y=|cot
) (D).y=|cot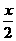 |
|
(3).过点A(-2,0)和B(2,3)的直线l的倾斜角为α,则cosα= ( )
(A).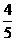 (B).
(B).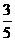 (C).-
(C).-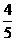 (D).-
(D).-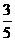
(4).设等差数列{an}的前n项和为Sn若a1>0, S4=S8,则Sn当取得最大值时,n的值为 ( )
(A).5 (B).6 (C).7 (D).8
(5).已知A、B、C三点在一条直线上,且A(3,-6),B(-5,2),若点C的横坐标为6,
则点C的纵坐标为 ( )
(A).-13 (B).9 (C).-9 (D).13
(6).向量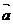 =(1,-2),向量
=(1,-2),向量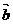 与
与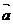 共线,且|
共线,且|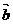 |=4|
|=4|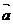 |,则
|,则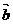 = ( )
= ( )
(A).(-4,8) (B).(-4,8)或(4,-8)
(C).(4,-8) (D).(8,4)或(4,8)
(7).设x>-1,则函数y=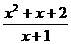 的最小值是 ( )
的最小值是 ( )
(A).2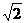 (B).2
(B).2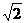 +1 (C).2
+1 (C).2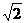 -1 (D).以上都不对
-1 (D).以上都不对
(8).下列各组中,M是N的充要条件的是 ( )
(A).M:|x|+|y|≤1,N:x2+y2≤1
(B).M:实数a、b,a+b>2,且ab>1,N:a>1且b>1
(C).M:集合E、F和P,P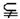 E且P
E且P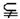 F,N:P
F,N:P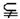 E∩F
E∩F
(D).M:-3≤t≤3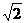 ,N:曲线y=
,N:曲线y=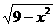 (y≠0)与直线y=x+t有公共点
(y≠0)与直线y=x+t有公共点
(9).给出下列命题:
①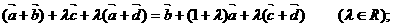
②把正方形ABCD平移向量 到A′B′C′D′的轨迹形成的几何体叫做正方体;
到A′B′C′D′的轨迹形成的几何体叫做正方体;
③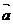 =“从济南往正比平移3km”,
=“从济南往正比平移3km”,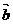 =“从济南向正北平移6km”,则
=“从济南向正北平移6km”,则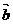 =2
=2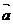 .
.
其中正确的命题是 ( )
(A).①② (B).②③ (C).①②③ (D).①③
(10).某商品的零售价2000年比1999年上涨25%,欲控制2001年比1999年只上涨10%,则2001年应比2000年降价 ( )
(A).15% (B).12% (C).10% (D).5%
(11).已知图①中的图象对应的函数y=f(x),则图②对应的函数在下列给出的四个式子中,只可能是 ( )
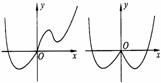 (A).y=f(x) B.y=|f(x)|
(A).y=f(x) B.y=|f(x)|
C.y=f(-|x|) D.y=-f(|x|)
(12).若0<a<1,函数f(x)=|logax|,则下列各式中成立的是 ( )
(A).f(2)>f(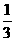 )>f(
)>f(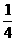 )
(B).f(
)
(B).f(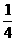 )>f(2)>f(
)>f(2)>f(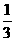 )
)
(C).f(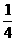 )>f(
)>f(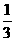 )>f(2) (D).f(
)>f(2) (D).f(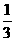 )>f(2) >f(
)>f(2) >f(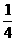 )
)
第Ⅱ卷(非选择题 共90分)
22. (本题满分14分)已知a>0,函数y=f(x)=x3
–ax在x∈ 是一个单调函
是一个单调函
数,
⑴ 试问函数y=f(x)在a>0的条件下,在x∈ 上能否是单调递减函数?请说
上能否是单调递减函数?请说
明理由;
⑵ 若f(x)在区间 上是单调递增函数,试求出实数a的取值范围;
上是单调递增函数,试求出实数a的取值范围;
⑶ 设x0≥1,f(x0)≥1且f[f(x0)]=x0,求证:f(x0)=x0.
21.(本题满分14分)如图,已知A,B,C是长轴长为4的椭圆上的三点,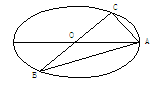 点A是长
点A是长
轴的一个端点,BC过椭圆中心O,且满足AC⊥BC,|BC|=2|AC|.
⑴ 建立适当的坐标系,求椭圆的方程;
⑵ 如果P、Q是该椭圆上异于A、B的两点,使∠PCQ的平分线垂直于OA,
求证:PQ∥AB.
20.(本题满分12分)猎人射击距离100米远处的目标,命中的概率为0.6。
(1)如果猎人射击距离100米远处的静止目标3次,求至少有一次命中的概率;
(2)如果猎人射击距离100米远处的动物,假如第一次未命中,则进行第二次射击,但由于枪声惊动动物使动物逃跑从而使第二次射击时动物离猎人的距离变为150米,假如第二次仍未命中,则必须进行第三次射击,而第三次射击时动物离猎人的距离为200米。假如击中的概率与距离成反比,。求猎人最多射击三次命中动物的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com