
题目列表(包括答案和解析)
7.若 且函数
且函数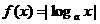 ,则下列各式中成立的是(D)
,则下列各式中成立的是(D)
(A)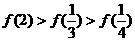 (B)
(B)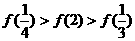
(C)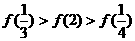 (D)
(D)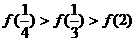
6.二面角α-a-β的平面角为120°,在面α内,AB⊥a于B,AB=2在平面β内,CD⊥a于D,CD=3,BD=1,M是棱a上的一个动点,则AM+CM的最小值为 (C)
A.2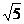 B.2
B.2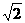 C.
C. D.2
D.2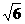
5.从5双不同的袜子中任取4只,使至少有2只袜子配成一双的可能取法种数是(C)
A.20 B.30 C.130 D.140
4.甲射手射击一次,击中目标的概率是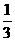 ;乙射手射击一次,击中目标的概率是
;乙射手射击一次,击中目标的概率是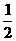 . 甲、乙两射手各射击一次,那么
. 甲、乙两射手各射击一次,那么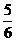 是 (D)
是 (D)
A.甲、乙两射手都击中目标的概率 B.甲、乙两射手都没有击中目标的概率
C.甲、乙恰有一射手击中目标的概率 D.甲、乙两射手没有都击中目标的概率
3.球面上有3个点,其中任意两点的球面积距离都等于大圆周长的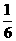 ,经过这三点的小圆周长为4π,那么这个球的半径为 (B)
,经过这三点的小圆周长为4π,那么这个球的半径为 (B)
A.4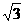 B.2
B.2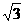 C.2 D.
C.2 D.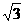
2.某博物馆要在7天内接待3所学校的学生参观,每天只安排一所学校,其中一所人数较多的学校要连续参观3天,其余学校均只参观1天,则在这7天内不同的安排方法共有( B)
A.30种 B.60种 C.120种 D.210种
1.从P点出发的三条射线PA、PB、PC两两成60°角,则PC与面PAB所成角的余弦值为( B)
A.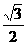 B.
B.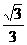 C.
C. D.以上都不对
D.以上都不对
4、重视解题思维习惯的形成
养成良好的思维习惯,可避免小题大做,少走弯路。如求角度值时应:找角--作角--转移角--用向量计算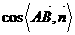 ;即先找现成的角,看看是否就是要求的角,不是的话试着作角,作角有难度的话通过平移转移角,实在不行用“数”解。类似的,求距离时应找高线--作高线--按比例转移--用向量计算等。
;即先找现成的角,看看是否就是要求的角,不是的话试着作角,作角有难度的话通过平移转移角,实在不行用“数”解。类似的,求距离时应找高线--作高线--按比例转移--用向量计算等。
总之,空间向量在立几中的应用,特别是用数量积求异面直线所成的角、斜线和平面所成的角、二面角的平面角;用向量在法向量上的投影求点到平面的距离,异面直线间的距离;用待定系数法求解立几开放题、探索题等。确实体现了它的强大功能。但不可否认,传统方法也有它的优越性,一旦空间的位置关系搞清楚了,计算量较小,正确率高。这“数”和“形”两条路应正确理解,合理选择。
3、重视常规思路在解题中的应用
解立体几何题的一大难点是如何添加辅助线,而如何添加辅助线有一定规律。如:线段中点--用中位线;三角形等腰--底边上的中线垂直底边;两直线异面--平移为相交直线;具有面的垂线--用三垂线定理或逆定理;线面平行,面面垂直--用性质定理;同一点出发三直线两两垂直--建立空间直角坐标系等。这些常规通过讲练应使学生熟练掌握。
2、重视常见体在解题中的利用
著名数学家波利亚指出:试着解决一个容易着手的简单问题,特殊的问题,类似的问题。立体几何中也是如此,一些具有特殊条件问题利用特殊体去解决能使解题简捷明快。如正四面体可在正方体中截得,三射线两两垂直、锐角在一个平面上的射影为直角时可在长方体里找到,空间四射线两两夹角相等可在正四面体找到等。
 [例7](2003全国高考)一个四面体的所有棱长都为
[例7](2003全国高考)一个四面体的所有棱长都为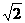 ,四个顶点在同一球面上,则此球的表面积为A.3π B.4π C.
,四个顶点在同一球面上,则此球的表面积为A.3π B.4π C.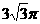 D.6π
D.6π
简析:棱长为1的正方体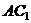 中,连接面对角线
中,连接面对角线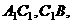
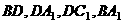 得到四面体
得到四面体 各棱长为
各棱长为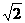 ,
,
从而得到球直径为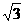 。
。
[例8](教科书复习参考题九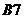 )
)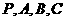 是球面上四点,
是球面上四点,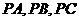 两两垂直,且
两两垂直,且
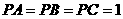 ,求球的体积和面积。
,求球的体积和面积。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com