
题目列表(包括答案和解析)
1.从集合M={不大于10的正自然数}中,选取三个数,使这三个数组成公差d=-3的等差数列,则这样的等差数列一共有
(A)2个 (B)3个 (C)4个 (D)5个
22.(理)(本小题满分14分)已知函数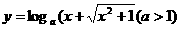 的反函数为f(x).
的反函数为f(x).
(Ⅰ)若f(x)<f(1),求x的取值范围;
(Ⅱ)判断f(2)与2f(1);f(3)与3f(1)的大小关系,并加以证明;
(Ⅲ)请你根据(Ⅱ)归纳出一个更一般的结论,并给予证明.
(文)设f(x)是定义在[-1,1)上的偶函数,f(x)与g(x)的图像关于直线x-1=0对称,且当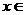 [2,3]时,g(x)=a(x-2)-2(x-2)3(a为常数).
[2,3]时,g(x)=a(x-2)-2(x-2)3(a为常数).
(Ⅰ)求f(x)的解析式;
(Ⅱ)若f(x)在[0,1]上是增函数,求实数a的取值范围;
(Ⅲ)若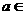 (一6,6),问能否使f(x)的最大值为4.
(一6,6),问能否使f(x)的最大值为4.
21.(本小题满分12分)
已知双曲线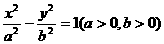 的左、右焦点分别为F1、F2,点P在双曲线的右支上,且:|PF1|=3|PF2|.
的左、右焦点分别为F1、F2,点P在双曲线的右支上,且:|PF1|=3|PF2|.
(Ⅰ)求离心率e的最值,并写出此时双曲线的渐近线方程;
(Ⅱ)若当点P的坐标为(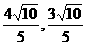 )时,
)时,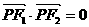 .求双曲线的方程.
.求双曲线的方程.
20.(理)(本小题满分12分)
设f(x)是定义在[-1,1]上的偶函数,f(x)与g(x)的图像关于x-1=0对称,且当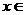 [2,3]时,g(x)=a(x-2)-2(x-2)3(a为常数).
[2,3]时,g(x)=a(x-2)-2(x-2)3(a为常数).
(Ⅰ)求f(x)的解析式;
(Ⅱ)若f(x)在[0,1]上是增函数,求实数a的取值范围;
(Ⅲ)若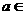 (-6,6),问能否使f(x)的最大值为4.
(-6,6),问能否使f(x)的最大值为4.
(文)已知函数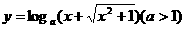 的反函数是f(x).
的反函数是f(x).
(Ⅰ)求f(x)的解析式;
(Ⅱ)若f(x)<f(1),求x的取值范围;
(Ⅱ)判断f(3)与3f(1)的大小关系,并加以证明.
19.(甲)(本小题满分12分)
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别是D1D、DB的中点,G在棱CD上.CG=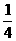 CD,H是C1G的中点,用向量方法解决下列问题:
CD,H是C1G的中点,用向量方法解决下列问题:
(Ⅰ)求证:EF⊥B1C;
(Ⅱ)求EF与C1G所成角的余弦值;
(Ⅲ)求FH的长.
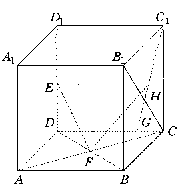
(乙)(本小题满分12分)
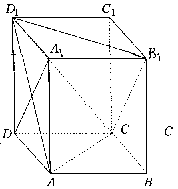
如图,在直四棱柱ABCD-A1B1C1D1中,底面是边长为a的菱形,侧棱长为2a.
(Ⅰ)问B1D1:与A1D能否垂直?并证明你的结论;
(Ⅱ)若∠ABC=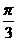 ,求二面角D1-AC-B1的大小;
,求二面角D1-AC-B1的大小;
(Ⅲ)当∠ABC在[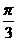 ,
,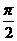 ]上变化时,求异面直线AC1与A1B1所成角的取值范围.
]上变化时,求异面直线AC1与A1B1所成角的取值范围.
18.(本小题满分12分)
设一次函数f(x)的图像关于直线y=x对称的图像为C,且f(-1)=0.若点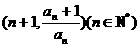 在曲线C上,并有a1=a2=1.
在曲线C上,并有a1=a2=1.
(Ⅰ)求曲线C的方程;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)设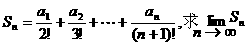 的值.
的值.
(文科生不作第(Ⅲ)问)
注意:考生在(19甲)、(19乙)两题中选一题作答,如果两题都答,只以(19甲)计分.
17.(本小题满分12分)
有一批食品出厂前,要进行五项指标抽检,如果有两项指标不合格,则这批食品不能出厂.已知每项指标抽检是相互独立的,且每项抽检出现不合格的概率都是0.2.
(Ⅰ)求这批食品不能出厂的概率(保留三位有效数字);
(Ⅱ)求直至五项指标全部检验完毕,才能确定该批食品是否出厂的概率(保留三位有效数字).
16.给出下列四个命题:
①若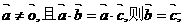 ②若
②若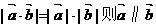 ;③在△ABC中,a=5,b=8,c=7,则=20;④设A(4,a),B(b,8),C(a,b),若OABC是平行四边形(O为原点),则∠AOC=
;③在△ABC中,a=5,b=8,c=7,则=20;④设A(4,a),B(b,8),C(a,b),若OABC是平行四边形(O为原点),则∠AOC=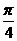 .其中真命题的序号是
.
.其中真命题的序号是
.
15.已知函数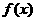 是偶函数,且在(一∞,c)上为增函数,又f(-3)=0,则满足
是偶函数,且在(一∞,c)上为增函数,又f(-3)=0,则满足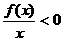 的x的取值范围是_________。
的x的取值范围是_________。
14.点P在曲线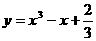 上移动,设过点P的切线的倾斜角为α,则α的取值范围是
.
上移动,设过点P的切线的倾斜角为α,则α的取值范围是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com