
题目列表(包括答案和解析)
5.欲对某商场作一简要审计,通过检查发票及销售记录的2%来快速估计每月的销售总额。现采用如下方法:从某本50张的发票存根中随机抽一张,如15号,然后按序往后将65号,115号,165号,…发票上的销售额组成一个调查样本。这种抽取样本的方法是( )
A.简单随机抽样 B.系统抽样 C.分层抽样 D.其它方式的抽样
4.双曲线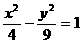 的渐近线方程是( )
的渐近线方程是( )
A. 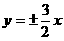 B.
B. 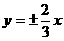 C.
C. 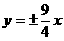 D.
D. 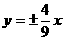
3.已知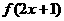 的最大值为2,
的最大值为2,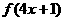 的最大值为
的最大值为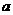 ,则
,则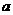 的取值范围是( )
的取值范围是( )
A.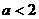 B.
B.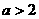 C.
C.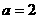 D.以上三种均有可能
D.以上三种均有可能
2.设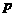 :
: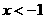 ,
,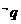 :
: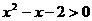 ,则下列命题为真的是( )
,则下列命题为真的是( )
A.若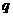 则
则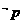 B.若
B.若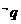 则
则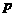 C.若
C.若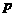 则
则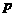 D.若
D.若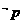 则
则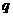
1.在函数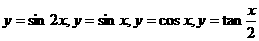 中,最小正周期为
中,最小正周期为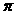 的函数是( )
的函数是( )
A. 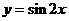 B.
B. 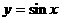 C.
C. 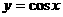 D.
D. 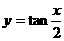
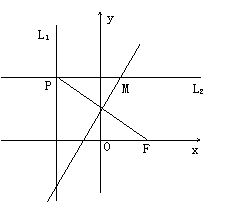
20.如图,设定直线L1:x=-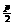 ,定点F(
,定点F(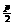 ,0),其中
,0),其中 >0.动直线L2垂直L1与点P,线
>0.动直线L2垂直L1与点P,线
段PF的垂直平分线交L2与点M。
(1)求点M的轨迹C的方程。
(2)设点M的轨迹C与x轴交于点Q,在C上是否一定存在另外两点R、S,使得ΔQRS
 为等边三角形?若存在,请用
为等边三角形?若存在,请用 表示这个等边三角形的面积;若不存在,请说明理由。
表示这个等边三角形的面积;若不存在,请说明理由。
解:
18.已知数列{an}中,a1=2、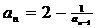 (n≥2),bn是方程(an+1)2x2-2(an+1)x+1=0的根;
(n≥2),bn是方程(an+1)2x2-2(an+1)x+1=0的根;
(1)探索数列{an}的通项公式并说明理由;
(2)设函数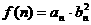 (nÎN),求
(nÎN),求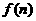 的最小值。
的最小值。
解:
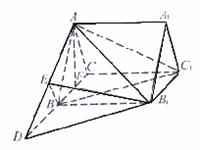
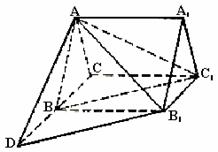 19.如图,正三棱柱ABC-A1B1C1的底面边长的3,侧棱AA1=
19.如图,正三棱柱ABC-A1B1C1的底面边长的3,侧棱AA1=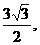 D是CB延长线上一点,且BD=BC.
D是CB延长线上一点,且BD=BC.
(Ⅰ)求证:直线BC1//平面AB1D;
(Ⅱ)求二面角B1-AD-B的大小;
(Ⅲ)求三棱锥C1-ABB1的体积.
(Ⅰ)证明:CD//C1B1,又BD=BC=B1C1,
∴ 四边形BDB1C1是平行四边形, ∴BC1//DB1.
又DB1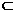 平面AB1D,BC1
平面AB1D,BC1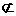 平面AB1D,
平面AB1D,
∴直线BC1//平面AB1D.
 (Ⅱ)解:过B作BE⊥AD于E,连结EB1,
(Ⅱ)解:过B作BE⊥AD于E,连结EB1,
∵B1B⊥平面ABD,∴B1E⊥AD ,
∴∠B1EB是二面角B1-AD-B的平面角,
∵BD=BC=AB,
∴E是AD的中点, 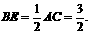
在Rt△B1BE中,
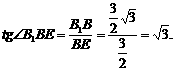 ∴∠B1EB=60°。即二面角B1-AD-B的大小为60°
∴∠B1EB=60°。即二面角B1-AD-B的大小为60°
(Ⅲ)解法一:过A作AF⊥BC于F,∵B1B⊥平面ABC,∴平面ABC⊥平面BB1C1C,
∴AF⊥平面BB1C1C,且AF=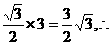
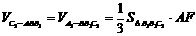
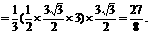 即三棱锥C1-ABB1的体积为
即三棱锥C1-ABB1的体积为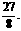
解法二:在三棱柱ABC-A1B1C1中,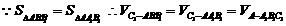
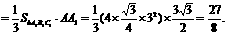 即三棱锥C1-ABB1的体积为
即三棱锥C1-ABB1的体积为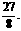
17.已知函数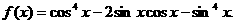
(Ⅰ)求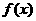 的最小正周期; (Ⅱ)若
的最小正周期; (Ⅱ)若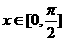 ,求
,求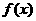 的最大值、最小值.
的最大值、最小值.
(Ⅰ)解:因为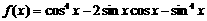
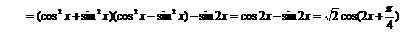
所以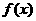 的最小正周期
的最小正周期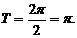
(Ⅱ)解:因为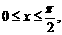 所以
所以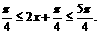 当
当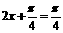 时,
时,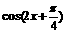 取得最大值
取得最大值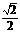 ;
;
当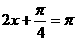 时,
时,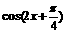 取得最小值-1.
取得最小值-1.
所以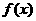 在
在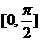 上的最大值为1,最小值为-
上的最大值为1,最小值为-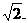
16. 某班试用电子投票系统选举班干部候选人.全班k名同学都有选举权和被选举权,他们的编号分别为1,2,…,k,规定:同意按“1”,不同意(含弃权)按“0”,令
 其中i=1,2,…,k,且j=1,2,…,k,则同时同意第1,2号同学当选的人数为( C )
其中i=1,2,…,k,且j=1,2,…,k,则同时同意第1,2号同学当选的人数为( C )
A.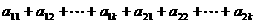
B.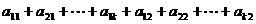
C.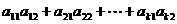
D.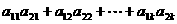
15.已知α,β是平面,m,n是直线.下列命题中不正确的是 ( B )
A.若m∥n,m⊥α,则n⊥α B.若m∥α,α∩β=n,则m∥n
C.若m⊥α,m⊥β,则α∥β D.若m⊥α,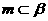 ,则α⊥β
,则α⊥β
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com