
题目列表(包括答案和解析)
2.设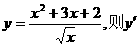 等于
等于
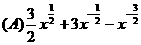

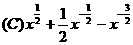

1.设f(x)=cosx,则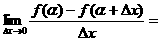
(A)sinα (B)-sinα (C)cosα (D)-cosα
22.解:(Ⅰ)设点.(x,y),由对称性得
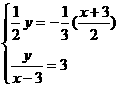 2分
2分
解得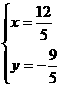 即点N的坐标为(
即点N的坐标为(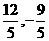 )
4分
)
4分
∵N(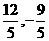 )不满足抛物线C的方程,
)不满足抛物线C的方程,
∴点N不在C上 6分
(Ⅱ)由y=kx与(y+1)2=3(x-1)消去y得
k2x2+(2k-3)x+4=0
∴l与C有公共点且k≠0,∴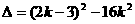 ≥0
≥0
解得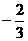 ≤k≤
≤k≤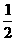 且k≠0
8分
且k≠0
8分
∵点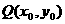 、
、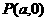 关于y=kx对称,
关于y=kx对称,
∴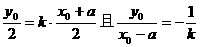 ,解得
,解得
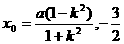 ≤k≤
≤k≤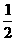 ,k≠0
10分
,k≠0
10分
当点Q在直线x=1上时,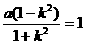 ,或
,或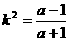
∵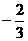 ≤k≤
≤k≤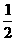 ,k≠0,∴0<k≤
,k≠0,∴0<k≤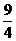 ,
,
∴0<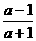 ≤
≤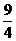 12分
12分
解得a≤-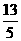 或a>1
14分
或a>1
14分
21.解:(Ⅰ)由题意: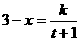 将
将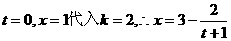 2分
2分
当年生产x(万件)时,年生产成本=年生产费用+固定费用=32x+3=32(3-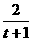 )+3,当销售x(万件)时,年销售收入=150%[32(3-
)+3,当销售x(万件)时,年销售收入=150%[32(3-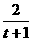 +3]+
+3]+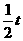
由题意,生产x万件化妆品正好销完
∴年利润=年销售收入-年生产成本-促销费
即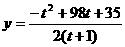 (t≥0)
6分
(t≥0)
6分
(Ⅱ)∵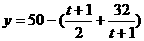 ≤50-
≤50-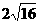 =42万件
10分
=42万件
10分
当且仅当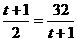 即t=7时,ymax=42
即t=7时,ymax=42
∴当促销费定在7万元时,利润增大. 12分
20.解:(Ⅰ)由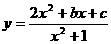 得
得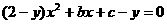 ,当y-2≠0,由x∈R,
,当y-2≠0,由x∈R,
有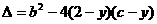 ≥0即
≥0即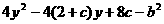 ≤0 ?2分
≤0 ?2分
由已知得2+c=1+3且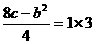
∴b=±2,c=2又b<0 ∴b=-2,c=2 5分
而y-2=0,b=-2,c=2代入*得x=0 6分
∴b=-2 c=2为所求 7分
(Ⅱ)取-1≤x1≤1
则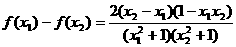
∵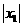 ≤1,|x2|≤1,x1<x2
≤1,|x2|≤1,x1<x2
∴|x1x2|<1,1-x1x2>0而x2-x1>0,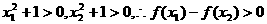
∴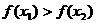
∴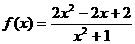 在[-1,1]上是减函数
12分
在[-1,1]上是减函数
12分
19.解:(Ⅰ)由题意2d=a3-a1=f(d+1)-f(d-1)=(d)2-(d-2)2
∴d=2.
a1=0.∴an=2n-2 3分
同理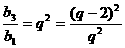
∴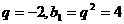 ∴
∴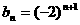
(Ⅱ)∵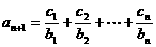 ,
,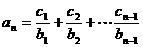
∴ 又∵
又∵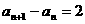 ,
,
∴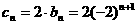
{cn}是首项为8,公比为-2的等比数列 9分
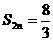 [1-(-2)2n],
[1-(-2)2n],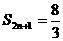 [1-(-2)2n+1?],
[1-(-2)2n+1?],
∴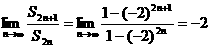 2分
2分
18.解:(Ⅰ)连结AC,则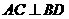 ,又AC是A1C在平面ABCD内的射影∴
,又AC是A1C在平面ABCD内的射影∴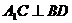 ;
;
又∵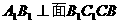 ,且A1C在平面
,且A1C在平面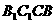 内的射影
内的射影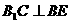 ,∴
,∴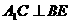 ,又∵
,又∵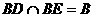 ∴
∴ 4分
4分
(Ⅱ)连结DF,A1D,∵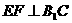 ,
,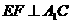 ,∴
,∴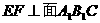 ,∴∠EDF即为ED与平面A1B1C所成的角 6分 由条件
,∴∠EDF即为ED与平面A1B1C所成的角 6分 由条件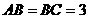 ,
,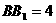 ,可知
,可知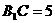 ,
,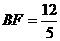 ,
,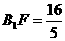 ,
,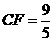 ,
,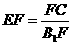 ·
·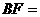
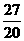 ,
,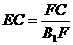 ·
·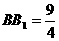
∴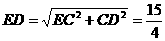 ∴
∴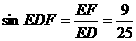 ∴ED与平面A1B1C所成角为arcsin
∴ED与平面A1B1C所成角为arcsin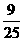 9分
9分
(Ⅲ)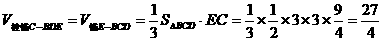 12分
12分
17.解:原不等式等价于(Ⅰ)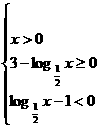
或(Ⅱ)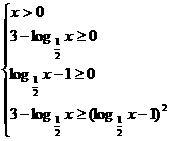 4分
4分
解(Ⅰ)得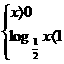 ∴x>
∴x>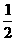 8分
8分
(Ⅱ)得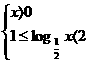 ?∴
?∴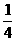 <x≤
<x≤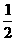 10分
10分
故原不等式的解集为{x|x>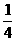 }12分
}12分
22.(本小题满分14分)
已知直线l:y=kx和抛物线C:(y+1)2=3(x-1).
(Ⅰ)k=-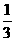 时,求点M(3,0)关于直线l的对称点N的坐标,并判断点N是否在抛物线C上.
时,求点M(3,0)关于直线l的对称点N的坐标,并判断点N是否在抛物线C上.
(Ⅱ)当k变化(k≠0)且直线l与抛物线C有公共点时,点P(a,0)关于直线l的对称点为Q(x0,y0),请写出x0关于k的函数关系式x0=f(k),并求出点Q在直线x=1上时a的取值范围.
第三次模拟测试
21.(本小题满分12分)
某化妆品生产企业为了占有更多的市场份额,拟在2002年度进行一系列促销活动,经过市场调查和测算,化妆品的年销量x万件与年促销t万元之间满足3-x与t+1成反比例,如果不搞促销活动,化妆品的年销量只能是1万件,已知2002年生产化妆品的设备折旧,维修等固定费用为3万元,每生产1万件化妆品需再投入32万元的生产费用,若将每件化妆品的售价定为:其生产成本的150%“与平均每件促销费的一半”之和,则当年生产的化妆品正好能销完.
(Ⅰ)将2002年的利润y(万元)表示为促销费t(万元)的函数;
(Ⅱ)该企业2002年的促销费投入多少万元时,企业的年利润最大?
(注:利润=销售收入-生产成本-促销费,生产成本=固定费用+生产费用)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com