
题目列表(包括答案和解析)
4.直线l1∥l2,l1上取3点,l2上取2点,由这五个点能确定的平面的个数是
A.1 B.3 C.6 D.9
3.四条线段顺次首尾相接,它们所在的直线最多可以确定的平面的条数是
A.4 B.3 C.2 D.1
2.空间交于一点的四条直线最多可以确定的平面的个数是
A.4 B.5 C.6 D.7
1.三条平行线所确定的平面的个数是
A.三个 B.两个 C.一个 D.一个或三个
21.设 上任一点,
上任一点, ∴曲线在
∴曲线在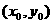 处的切线方程为
处的切线方程为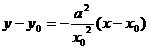 ,令x=0,求得切线在y轴上的切距为
,令x=0,求得切线在y轴上的切距为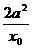 ,故切线与y轴的交点为
,故切线与y轴的交点为
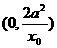 ,令y=0得切线与x轴的交点为
,令y=0得切线与x轴的交点为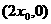 ∴切线与两坐标轴围成的三角形面积等于
∴切线与两坐标轴围成的三角形面积等于
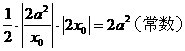
20.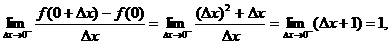
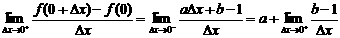 若b≠1,则
若b≠1,则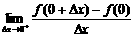
不存在∴b=1,又∵f(x)在x=0处可导∴a=1
19.由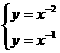 ,解得两曲线的交点为(1,1)。设两曲线在交点处的切线斜率分别为
,解得两曲线的交点为(1,1)。设两曲线在交点处的切线斜率分别为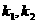 ,则
,则
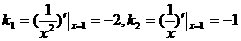 由两直线的夹角公式得tanα=
由两直线的夹角公式得tanα=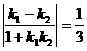
18.设切点为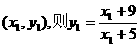 ①∴
①∴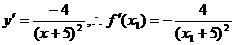 设所求的切线方程为 y=kx 则
设所求的切线方程为 y=kx 则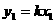 ②又k=
②又k=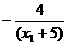 ③由①②③解得
③由①②③解得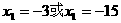
易得切点为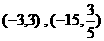 ,故所求的切线方程为x+y=0或x+25y=0
,故所求的切线方程为x+y=0或x+25y=0
20.已知函数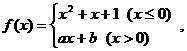 若f(x)在x=0处可导,求a,b的值
若f(x)在x=0处可导,求a,b的值
21*.求证:双曲线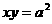 在任一点处的切线与两坐标轴构成的三角形面积等于常数
在任一点处的切线与两坐标轴构成的三角形面积等于常数
答案:一、ABCDD ABCCB BA;二、13、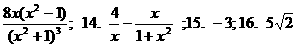
19.设曲线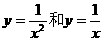 在它们交点处的两切线的夹角为α,求tanα
在它们交点处的两切线的夹角为α,求tanα
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com