
题目列表(包括答案和解析)
21.[解](1)设 得
得
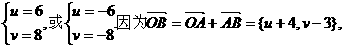
所以v-3>0,得v=8,故 ={6,8}.
={6,8}.
(2)由 ={10,5},得B(10,5),于是直线OB方程:
={10,5},得B(10,5),于是直线OB方程:
由条件可知圆的标准方程为:(x-3)2+y(y+1)2=10,
得圆心(3,-1),半径为 .
.
设圆心(3,-1)关于直线OB的对称点为(x ,y)则
 故所求圆的方程为(x-1)2+(y-3)2=10.
故所求圆的方程为(x-1)2+(y-3)2=10.
(3)设P (x1,y1), Q (x2,y2) 为抛物线上关于直线OB对称两点,则

故当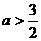 时,抛物线y=ax2-1上总有关于直线OB对称的两点.
时,抛物线y=ax2-1上总有关于直线OB对称的两点.
20.[解](1)如图建立直角坐标系,则点P(11,4.5), 椭圆方程为 .
.
 将b=h=6与点P坐标代入椭圆方程,得
将b=h=6与点P坐标代入椭圆方程,得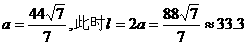 .因此隧道的拱宽约为33.3米.
.因此隧道的拱宽约为33.3米.
(2)[解一]
由椭圆方程 ,得
,得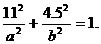

故当拱高约为6.4米、拱宽约为31.1米时,土方工程量最小.
[解二]由椭圆方程 ,得
,得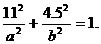 于是
于是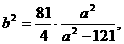
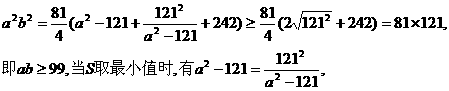
得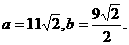 以下同解一.
以下同解一.
19.[解](1)

(2)归纳概括的结论为:
若数列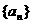 是首项为a1,公比为q的等比数列,则
是首项为a1,公比为q的等比数列,则

18.[解]连结BD,因为B1B⊥平面ABCD,B1D⊥BC,所以BC⊥BD.
 在△BCD中,BC=2,CD=4,所以BD=
在△BCD中,BC=2,CD=4,所以BD= .
.
又因为直线B1D与平面ABCD所成的角等于30°,所以
∠B1DB=30°,于是BB1= BD=2.
BD=2.
故平行六面体ABCD-A1B1C1D1的体积为SABCD·BB1= .
.
17.[解]

故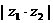 的最大值为
的最大值为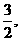 最小值为
最小值为 .
.
10.2.6 . 11.4π 12.|PF2|=17.
7.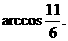 8.
8. 的一组数). 9.
的一组数). 9.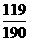
1.π. 2. . 3.-49 . 4.
. 3.-49 . 4. . 5.arctg2. 6.[1,3].
. 5.arctg2. 6.[1,3].
22.(本题满分18分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分7分.
已知集合M是满足下列性质的函数f(x)的全体:存在非零常数T,对任意x∈R,有f(x+T)=T f(x)成立.
(1)函数f(x)= x 是否属于集合M?说明理由;
(2)设函数f(x)=ax(a>0,且a≠1)的图象与y=x的图象有公共点,证明:
f(x)=ax∈M;
(3)若函数f(x)=sinkx∈M ,求实数k的取值范围.
普通高等学校招生全国统一考试(上海卷)
数学(理工农医类)答案
21.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分5分,第3小题满分7分.
在以O为原点的直角坐标系中,点A(4,-3)为△OAB的直角顶点.已知|AB|=2|OA|,且点B的纵坐标大于零.
(1)求向量 的坐标;
的坐标;
(2)求圆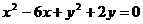 关于直线OB对称的圆的方程;
关于直线OB对称的圆的方程;
(3)是否存在实数a,使抛物线 上总有关于直线OB对称的两个点?若不存在,说明理由:若存在,求a的取值范围.
上总有关于直线OB对称的两个点?若不存在,说明理由:若存在,求a的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com