
题目列表(包括答案和解析)
6.函数y=2-x+1(x>0)的反函数是
?A.y=log2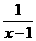 ,x∈(1,2)
,x∈(1,2)
?B.y=-log2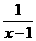 ,x∈(1,2)
,x∈(1,2)
? C.y=log2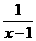 ,x∈(1,2)
,x∈(1,2)
? D.y=-log2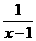 ,x∈(1,2]
,x∈(1,2]
5.已知复数z= ,则arg
,则arg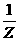 是
是
A.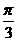 B.
B.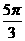 C.
C.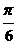 ?D.
?D.
4.若定义在区间(-1,0)内的函数f(x)=log2a(x+1)满足f(x)>0,则a的取值范围是
? A.(0,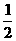 ) ?B.(0,
) ?B.(0,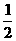 ] ?C.(
] ?C.(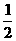 ,+∞) D.(0,+∞)
,+∞) D.(0,+∞)
3.极坐标方程ρ2cos2θ=1所表示的曲线是
?A.两条相交直线?B.圆 ?C.椭圆 ?D.双曲线
2.若一个圆锥的轴截面是等边三角形,其面积为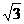 ,则这个圆锥的全面积是
,则这个圆锥的全面积是
?A.3π ? B.3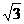 π ?C.6π? D.9π
π ?C.6π? D.9π
1.不等式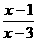 >0的解集为
>0的解集为
? A.{x|x<1} ?B.{x|x>3}
? C.{x|x<1或x>3} ?D.{x|1<x<3}
(17)本小题主要考查三角函数的图象和性质,考查利用三角公式进行恒等变形的技能以及运算能力。满分12分。
解:(I)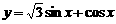
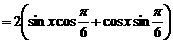
 ,
, 。
--3分
。
--3分
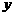 取得最大值必须且只需
取得最大值必须且只需
 ,
,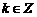 ,
,
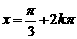 ,
,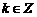 。
。
所以,当函数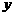 取得最大值时,自变量
取得最大值时,自变量 的集合为
的集合为
 。
--6分
。
--6分
(II)变换的步骤是:
(i) 把函数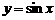 的图象向左平移
的图象向左平移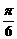 ,得到函数
,得到函数
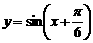 的图象;
--9分
的图象;
--9分
(ii) 令所得到的图象上各点横坐标不变,把纵坐标伸长到原来的2倍),得到函数
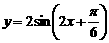 的图象;
的图象;
经过这样的变换就得到函数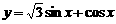 的图象。 --12分
的图象。 --12分
(18)本小题主要考查等差数列的基础知识和基本技能,运算能力。满分12分。
解:设等差数列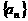 的公差为
的公差为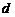 ,则
,则
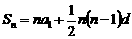
∵ 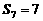 ,
,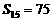 ,
,
∴ 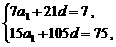 --6分
--6分
即 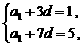
解得 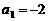 ,
, 。
--8分
。
--8分
∴ 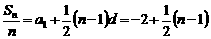 ,
,
∵ 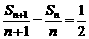 ,
,
∴
数列 是等差数列,其首项为
是等差数列,其首项为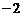 ,公差为
,公差为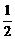 ,
,
∴
 。
--12分
。
--12分
(19)本小题主要考查直线与直线、直线与平面的关系,逻辑推理能力。满分
12分。
 (I)证明:连结
(I)证明:连结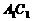 、AC,AC和BD交于O,连结
、AC,AC和BD交于O,连结 。
。
∵ 四边形ABCD是菱形,
∴ AC⊥BD,BC=CD。
又∵ 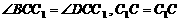 ,
,
∴  ,
,
∴  ,
,
∵ DO=OB,
∴ 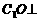 BD,
--3分
BD,
--3分
但 AC⊥BD,AC∩ =O,
=O,
∴ BD⊥平面 。
。
又 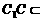 平面
平面 ,
,
∴ 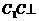 BD。
--6分
BD。
--6分
(II)当 时,能使
时,能使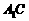 ⊥平面
⊥平面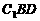 。
。
证明一:
∵  ,
,
∴ BC=CD=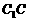 ,
,
又 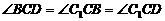 ,
,
由此可推得BD= 。
。
∴ 三棱锥C- 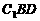 是正三棱锥。
--9分
是正三棱锥。
--9分
设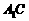 与
与 相交于G。
相交于G。
∵ 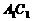 ∥AC,且
∥AC,且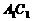 ∶OC=2∶1,
∶OC=2∶1,
∴  ∶GO=2∶1。
∶GO=2∶1。
又  是正三角形
是正三角形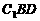 的BD边上的高和中线,
的BD边上的高和中线,
∴ 点G是正三角形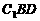 的中心,
的中心,
∴ CG⊥平面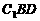 。
。
即 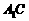 ⊥平面
⊥平面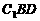 。
--12分
。
--12分
证明二:
由(I)知,BD⊥平面 ,
,
∵ 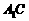
 平面
平面 ,∴ BD⊥
,∴ BD⊥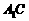 。
--9分
。
--9分
当  时 ,平行六面体的六个面是全等的菱形,
时 ,平行六面体的六个面是全等的菱形,
同BD⊥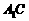 的证法可得
的证法可得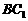 ⊥
⊥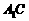 。
。
又 BD∩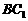 =B,
=B,
∴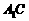 ⊥平面
⊥平面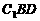 。
--12分
。
--12分
(20)本小题主要考查不等式的解法、函数的单调性等基本知识、分类讨论的
数学思想方法和运算、推理能力。满分12分。
解:(I)不等式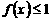 即
即
 ,
,
由此得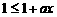 ,即
,即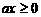 ,其中常数
,其中常数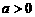 。
。
所以,原不等式等价于
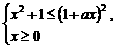
即 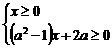 --3分
--3分
所以,当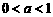 时,所给不等式的解集为
时,所给不等式的解集为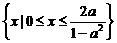 ;
;
当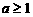 时,所给不等式的解集为
时,所给不等式的解集为 。 --6分
。 --6分
(II)在区间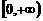 上任取
上任取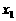 ,
, ,使得
,使得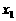 <
< 。
。

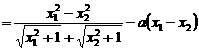
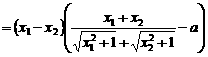 。 --9分
。 --9分
∵  ,且
,且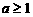 ,
,
∴  ,
,
又  ,
,
∴ 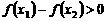 ,
,
即 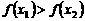 。
。
所以,当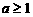 时,函数
时,函数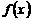 在区间
在区间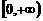 上是单调递减函数。 --12分
上是单调递减函数。 --12分
(21)本小题主要考查函数图象建立的函数关系式和求函数最大值的问题,考查运用所学知识解决实际问题的能力。满分12分。
解:(I)由图一可得市场售价与时间的函数关系为
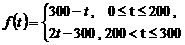 --2分
--2分
由图二可得种植成本与时间的函数关系为
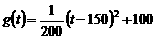 ,
, 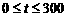 --4分
--4分
(II)设 时刻的纯收益为
时刻的纯收益为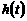 ,则由题意得
,则由题意得
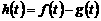 ,
,
即  --6分
--6分
当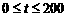 时,配方整理得
时,配方整理得
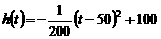 ,
,
所以,当 =50时,
=50时,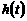 取得区间
取得区间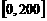 上的最大值100;
上的最大值100;
当 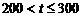 时,配方整理得
时,配方整理得
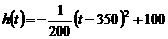 ,
,
所以,当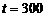 时,
时,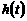 取得区间
取得区间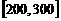 上的最大值87.5;--10分
上的最大值87.5;--10分
综上,由100>87.5可知,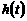 在区间
在区间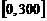 上可以取最大值100,此时,
上可以取最大值100,此时, 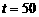 ,即从二月一日开始的第50天时,上市的西红柿纯收益最大。
,即从二月一日开始的第50天时,上市的西红柿纯收益最大。
--12分
(22)本小题主要考查坐标法、定比分点坐标公式、双曲线的概念和性质,推
理、运算能力和综合运用数学知识解决问题的能力。满分14分。
解:如图,以AB为垂直平分线为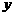 轴,直线AB为
轴,直线AB为 轴,建立直角坐标系
轴,建立直角坐标系 ,则CD⊥
,则CD⊥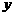 轴。
轴。
因为双曲线经过点C、D,且以A、B为焦点,由双曲线的对称性知C、D关于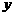 轴对称。
--2分
轴对称。
--2分
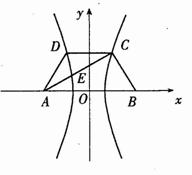 依题意,记A
依题意,记A ,B
,B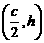 ,C
,C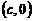 ,其中
,其中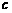 为双曲线的半焦距,
为双曲线的半焦距,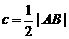 ,
,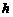 是梯形的高。
是梯形的高。
由定比分点坐标公式,得点E的坐标为
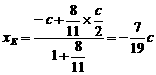 ,
,
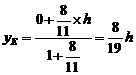 。
--5分
。
--5分
设双曲线的方程为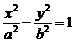 ,则离心率
,则离心率 。
。
由点C、E在双曲线上,得
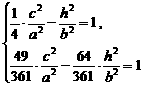 --10分
--10分
由①得 ,代入②得
,代入②得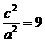 。
。
所以,离心率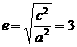 。
--14分
。
--14分
(13)252 (14) (15)
(15)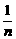 (16)②③
(16)②③
(1)C (2)B (3)D (4)D (5)D
(6)C (7)B (8)C (9)A (10)C
(11)C (12)D
未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com