
题目列表(包括答案和解析)
19.[解](1)当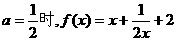 ,
,
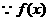 在区间
在区间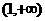 上为增函数,
…(3分)
上为增函数,
…(3分)
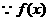 地区间
地区间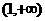 上最小值为
上最小值为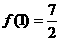 ,
…(6分)
,
…(6分)
(2)[解法一]在区让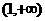 上,
上,
 恒成立,
…(8分)
恒成立,
…(8分)
设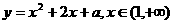 ,
,
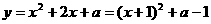 递增,∴当
递增,∴当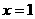 时,
时,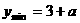 , …(12分)
, …(12分)
于是当且仅当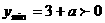 时,函数
时,函数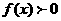 恒成立,
恒成立,
故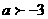 。
…(14分)
。
…(14分)
(2)[解法二]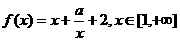 ,当
,当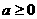 时,函数
时,函数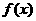 的值恒为正, …(8分)
的值恒为正, …(8分)
当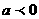 时,函数
时,函数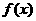 递增,故当
递增,故当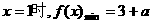 ,
…(12分)
,
…(12分)
于是当且仅当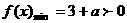 时,函数
时,函数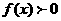 恒成立,故
恒成立,故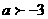 。
…(14分)
。
…(14分)
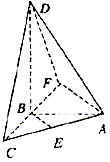
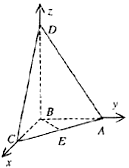
18.[解法一]如图建立空间直角坐标系 …(2分)
由题意,有A(0,2,0),C(2,0,0),E(1,1,0)。设D点的坐标为(0,0,z)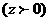 ,则
,则
 又
又
[解法二]过A引BE的平行线,交与CB的延长线于F,∠DAF是异面直线BE与AD所成的角,
∴∠DAF=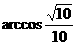 …(4分)
…(4分)
∵E是AC的中点,∴B是CF的中点,
AF=2BE=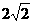 。
…(6分)
。
…(6分)
又BF,BA分别是DF,DA的射影,且BF=BC=BA。
∴DF=DA。 …(8分)
三角形ADF是等腰三角形,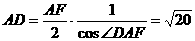 ,
,
故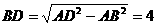 ,
…(10分)
,
…(10分)
又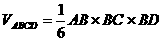 ,
,
因此四面体ABCD的体积是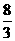 ,
…(12分)
,
…(12分)
17.[解]设椭圆C的方程为
由题意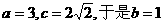

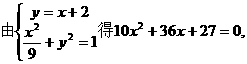
因为该二次方程的判别式△>0,所以直线与椭圆有两个不同交点, …(8分)
 设
设
1.4.
2.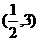 3.(-4,0),(6,0)。 4.
3.(-4,0),(6,0)。 4.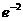 。 5.1.
6.9. 7.侧棱相等/侧棱与底面所成角相等/…… 8.X. 9.-462。 10.
。 5.1.
6.9. 7.侧棱相等/侧棱与底面所成角相等/…… 8.X. 9.-462。 10.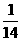 11.
11. 12.
12.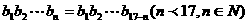
3.第17至第22题中右端所注的分数,表示考生正确做到这一步应得的该题的累加分数,给分或扣分均以1分为单位。
解答
2.评阅试卷,应坚持每题评阅以底,不要因为考生的解称中出现错误而中断对该题的评阅,当考生的解答在某一步出现错误,影响了后继部分,但该步以后的解答未改变这一题的内容和难度时,可视影响程度决定后面部分的给分,这时原则上不应超过后面部分应给分数之半,如果有较严重的概念性错误,就不给分。
1.本解答列出试题的一种或几种解法,如果考生的解法与所列解法不同,可参照解答中评分标准的精神进行评分。
22.(本小题满分18分)本题共有3个小题,第1小题满分5分,第2小题满分5分,第3小题满分8分。
已知复数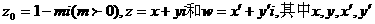 均为实数,
均为实数,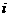 为虚数单位,且对于任意复数
为虚数单位,且对于任意复数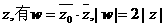 。
。
(1)试求 的值,并分别写出
的值,并分别写出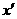 和
和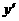 用
用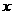 、
、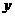 表示的关系式;
表示的关系式;
(2)将(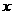 、
、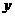 )作为点
)作为点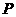 的坐标,(
的坐标,(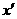 、
、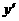 )作为点
)作为点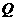 的坐标,上述关系可以看作是坐标平面上点的一个变换:它将平面上的点
的坐标,上述关系可以看作是坐标平面上点的一个变换:它将平面上的点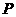 变到这一平面上的点
变到这一平面上的点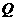 ,
,
当点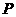 在直线
在直线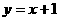 上移动时,试求点
上移动时,试求点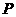 经该变换后得到的点
经该变换后得到的点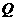 的轨迹方程;
的轨迹方程;
(3)是否存在这样的直线:它上面的任一点经上述变换后得到的点仍在该直线上?若存在,试求出所有这些直线;若不存在,则说明理由。
[解](1)
[解](2)
[解](3)
全国普通高等学校招生统一考试
答案要点及评分标准
说明
21.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分。
在XOY平面上有一点列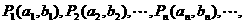 对每个自然数
对每个自然数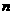 ,点
,点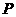 ,位于函数
,位于函数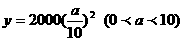 的图象上,且点
的图象上,且点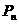 ,点
,点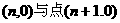 构成一个以
构成一个以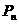 为顶点的等腰三角形。
为顶点的等腰三角形。
(1)求点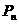 的纵坐标
的纵坐标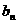 的表达式。
的表达式。
(2)若对每个自然数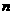 ,以
,以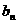 ,
,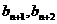 为边长能构成一个三角形,求
为边长能构成一个三角形,求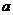 取值范围。
取值范围。
(3)设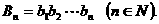 ,若
,若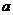 取(2)中确定的范围内的最小整数,求数列
取(2)中确定的范围内的最小整数,求数列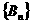 的最大项的项数。
的最大项的项数。
[解](1)
[解](2)
[解](3)
20.(本题满分14分)本题共有2个小题,第1小题满分4分,第2小题满分10分。
根据指令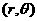
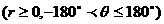 ,机器人在平面上能完成下列动作:先原地旋转角度
,机器人在平面上能完成下列动作:先原地旋转角度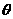 (
(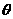 为正时,按逆时针方向旋转
为正时,按逆时针方向旋转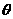 ,
,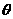 为负时,按顺时针方向旋转-
为负时,按顺时针方向旋转-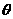 ),再朝其面对的方向沿直线行走距离
),再朝其面对的方向沿直线行走距离 。
。
(1)现机器人在直角坐标系的坐标原点,且面对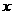 轴正方向,试给机器人下一个指令,使其移动到点(4,4)。
轴正方向,试给机器人下一个指令,使其移动到点(4,4)。
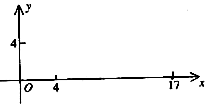 (2)机器人在完成该指令后,发现在点(17,0)处有一小球正向坐标原点作匀速直线滚动,已知小球滚动的速度为机器人直线行走速度的2倍,若忽略机器人原地旋转所需的时间,问机器人最快可在何处截住小球?并给出机器人截住小球所需的指令(结果精确到小数点后两位)。
(2)机器人在完成该指令后,发现在点(17,0)处有一小球正向坐标原点作匀速直线滚动,已知小球滚动的速度为机器人直线行走速度的2倍,若忽略机器人原地旋转所需的时间,问机器人最快可在何处截住小球?并给出机器人截住小球所需的指令(结果精确到小数点后两位)。
[解](1)
[解](2)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com