
题目列表(包括答案和解析)
7.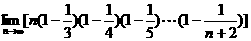 等于 ( )
等于 ( )
A.0 B.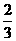 C.1 D.2
C.1 D.2
6.一质点在直线上从时刻t=0秒以速度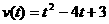 (米/秒)运动,则该质点在时刻
(米/秒)运动,则该质点在时刻
t=3秒时运动的路程为 ( )
A.4米 B.8米 C. D.
D.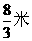
5.若某等差数列{an}中,a2+a6+a16为一个确定的常数,则其前n项和Sn中也为确定的常数
的是 ( )
A.S17 B.S15 C.S8 D.S7
4.已知数列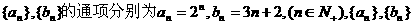 中相同项从小到大排成的新数列为{cn},则{cn}的第5项是 ( )
中相同项从小到大排成的新数列为{cn},则{cn}的第5项是 ( )
A.128 B.512 C.1024 D.2048
3.等差数列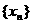 的前n项和为An,已知
的前n项和为An,已知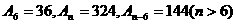 ,则n为( )
,则n为( )
A.18 B.17 C.16 D.15
2.设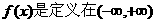 上的奇函数,且在区间(0,
上的奇函数,且在区间(0, )上单调递增,若
)上单调递增,若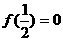 ,三角形的内角满足
,三角形的内角满足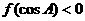 ,则A的取值范围是 ( )
,则A的取值范围是 ( )
A.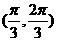 B.
B.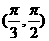
C.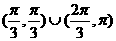 D.
D.
1.在等差数列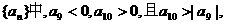 则在前n项和Sn中最大的负数为( )
则在前n项和Sn中最大的负数为( )
A.S16 B.S17
C.S18 D.S19
22.(本小题满分12分)
已知函数f(x-2)=ax2-(a-3)x+a-2(a<0,a∈Z)的图象与x轴有交点.
(1)求a的值;(2)求f(x)的解析式;
(3)若g(x)=1-[f(x)]2,F(x)=c·g(x)+d·f(x),问是否存在c(c>0),d使得在区间(-∞,f(2))内是单调递增函数,而在区间(f(2),0)内是单调递减函数?若存在,求c,d之间的关系,并写出推理过程;若不存在,说明理由.
解:
(1)a=-1;
(2)f(x)=-x2+1
(3)g(x)=-x4+2x2,F(x)=-cx4+(2c-d)x2+d(c>0).
若F(x)在(-∞,f(2)),即在(-∞,-3)上为增函数,则当x1<x2<-3时F(x2)-F(x1)>0,于是有(x22-x12)[-c(x12+x22)+2c-d]>0.
∵x22-x12<0,∴-c(x12+x22)+2c-d<0.
∴x12+x22>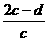 .
.
要使该式在(-∞,3)上恒成立,只须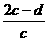 ≤(-3)2+(-3)2=18,即16c+d≥0,同样的方法可得,要使F(x)在(-3,0)上为减函数,只须16c+d≤0,因此当16c+d=0时满足给出的所有条件.
≤(-3)2+(-3)2=18,即16c+d≥0,同样的方法可得,要使F(x)在(-3,0)上为减函数,只须16c+d≤0,因此当16c+d=0时满足给出的所有条件.
另解:依题意,F(x)在x=-3时有极大值,
∵F′(x)=-4cx3+2(2c-d)x,
∴F′(x)|x=-3=0,同样可得16c+d=0.
21.(本小题满分12分)
设f(x)=ax2+bx+c(a>b>c),f(1)=0,g(x)=ax+b.
(1)求证:函数y=f(x)与y=g(x)的图象有两个交点;
(2)设f(x)与g(x)的图象交点A、B在x轴上的射影为A1、B1,求|A1B1|的取值范围;
(3)求证:当x≤-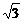 时,恒有f(x)>g(x).
时,恒有f(x)>g(x).
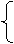 (1)证明: y=f(x)=ax2+bx+c
(1)证明: y=f(x)=ax2+bx+c
y=g(x)=ax+b 得ax2+(b-a)x+(c-b)=0
Δ=(b-a)2-4a(c-b)∵f(x)=ax2+bx+c,f(1)=0
∴f(1)=a+b+c=0又a>b>c ∴3a>a+b+c>3c即a>0,c<0
∴b-a<0,c-b<0,a>0∴Δ=(b-a)2-4a(c-b)>0
故函数y=f(x)与y=g(x)的图象有两个交点;
(2)解:设A、B的坐标分别为(x1,y1)、(x2,y2),
则x1、x2是方程(*)的两根故x1+x2=-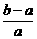 ,
,
x1x2=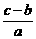 ,所以|A1B1|=|x1-x2|=
,所以|A1B1|=|x1-x2|=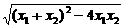
=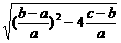 =
=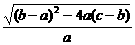 又a+b+c=0,故b=-(a+c)
又a+b+c=0,故b=-(a+c)
因而(b-a)2-4a(c-b)=(-2a-c)2-4a(a+2c)=c2-4ac
故|A1B1|=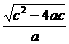 =
=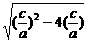 =
=
∵a>b>c,a+b+c=0∴a>-(a+c)>c
∴-2<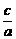 <-
<-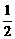 ∴|A1B1|的取值范围是(
∴|A1B1|的取值范围是(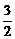 ,2
,2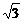 ).
).
(3)证明:不妨设x1>x2,则由(2)知:
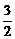 <x1-x2<2
<x1-x2<2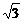 x1+x2=-
x1+x2=-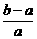 =1-
=1-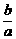 由a>b>c得:
由a>b>c得: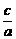 <
<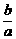 <1,
<1,
故0<1-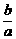 <1-
<1-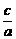 又-2<
又-2<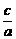 <-
<-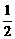 ,故
,故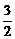 <1-
<1-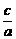 <3,
<3,
因而0<1-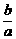 ≤
≤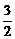 即0<x1-x2≤
即0<x1-x2≤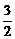 由①、②得:-
由①、②得:-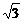 <x2≤0,
<x2≤0,
即方程(*),也就是方程f(x)-g(x)=0的较小根的范围是(-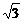 ,0].
,0].
又a>0,故当x≤-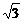 时,f(x)-g(x)>0恒成立,即当x≤-
时,f(x)-g(x)>0恒成立,即当x≤-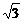 时,恒有f(x)>g(x).
时,恒有f(x)>g(x).
20.(本小题满分12分)
直线l:y=mx+1与椭圆C:ax2+y2=2交于A、B两点,以OA、OB为邻边作平行四边形OAPB(O为坐标原点)
(1)当a=2时,求点P的轨迹方程;
(2)当a,m满足a+2m2=1,且记平行四边形OAPB的面积函数S(a),求证:2<S(a)<4.
(1)解:设P(x,y),则OP中点为E(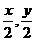 )
)
由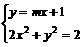 消去y得(2+m2)x2+2mx-1=0设A(x1,y1),B(x2,y2)
消去y得(2+m2)x2+2mx-1=0设A(x1,y1),B(x2,y2)
则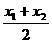 =-
=-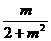 ,
,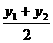 =m
=m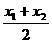 +1=
+1=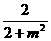
即AB的中点为E(-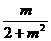 ,
,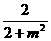 )
)
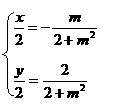
 于是
于是
消去m,得点P的轨迹方程为2x2+y2-2y=0
(2)证明:由消去y得(a+m2)x2+2mx-1=0进一步就可以求出|AB|=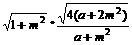
∵O到AB的距离d=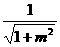 ·S(a)=|AB|d=
·S(a)=|AB|d=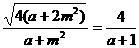
∵a+2m2=1∴0<a<1∴2<S(a)<4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com