
题目列表(包括答案和解析)
7.函数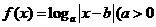 ,且
,且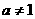 )是偶函数,且在
)是偶函数,且在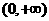 上单调递减,则
上单调递减,则
 与
与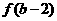 的大小关系是 ( )
的大小关系是 ( )
A. >
>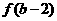 B.
B.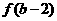


C.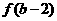

 D.
D. <
<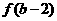
6. 已知
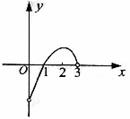
已知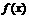 的定义在(-3,3)上的奇函数,当0<x<3时,
的定义在(-3,3)上的奇函数,当0<x<3时,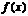 的图象如图所示,那么不等式
的图象如图所示,那么不等式 的解集是
( )
的解集是
( )
A.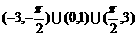 B.
B.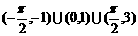
C.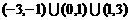 D.
D. 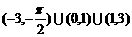
5.二次函数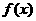 满足
满足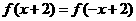 ,又
,又 ,若在
,若在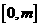 有最大值3,最小值1,则
有最大值3,最小值1,则 的取值范围是 ( )
的取值范围是 ( )
A.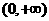 B.
B.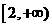 C.
C.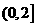 D.
D.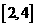
4.若x∈R、n∈N*,定义: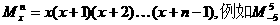 =(-5)(-4)
=(-5)(-4)
(-3)(-2)(-1)=-120,则函数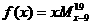 的奇偶性为 ( )
的奇偶性为 ( )
A.是偶函数而不是奇函数 B.是奇函数而不是偶函数
C.既是奇函数又是偶函数 D.既不是奇函数又不是偶函数
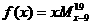 =x·(x-9)(x-8)x(x+8)[(x-9)+19-1]=x2(x2-9)…(x2-1).
=x·(x-9)(x-8)x(x+8)[(x-9)+19-1]=x2(x2-9)…(x2-1).
3.如果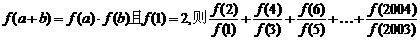 等于 ( )
等于 ( )
A.2003 B.1001 C.2004 D.2002
2.设随机变量ξ服从正态分布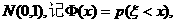 则下列结论不正确的是( )
则下列结论不正确的是( )
A.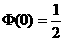 B.
B.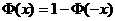
C.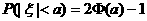 D.
D.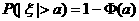
1.集合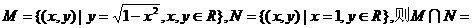 ( )
( )
A.{(1,0)} B.{y|0≤y≤1} C.{1,0} D.φ
22.(本题满分14分,附加题4分)
(Ⅰ)已知a>0,函数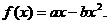
(1)当b>0时,若对任意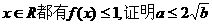 ;
;
(2)当b>1时,证明:对任意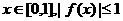 的充要条件是
的充要条件是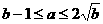 ;
;
解:(1)证明:由题设,对任意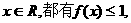 ∵
∵
∴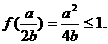 ∵a>0,b>0,
∵a>0,b>0,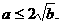
(2)证明:必要性:对任意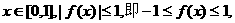 因此,
因此,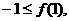
即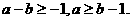 对任意
对任意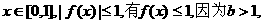
可推出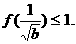 即
即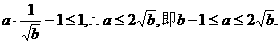
充分性:因为b>1,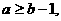 对任意
对任意 ,可以推出
,可以推出
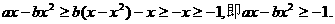
因为,b>1,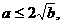 对任意
对任意 ,可以推出
,可以推出

综上,当b>1时,对任意 ,
,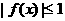 的充要条件是:
的充要条件是: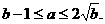
21.(本题满分12分)
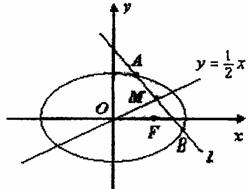 如图,过点(1,0)的直线l与中心在原点,焦点在x轴上且离心率为
如图,过点(1,0)的直线l与中心在原点,焦点在x轴上且离心率为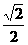 的椭圆相交于A、B两点,直线
的椭圆相交于A、B两点,直线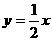 过线段AB的中点M,同时椭圆上存在一点与右焦点F关于直线l对称,求直线l和椭圆的方程.
过线段AB的中点M,同时椭圆上存在一点与右焦点F关于直线l对称,求直线l和椭圆的方程.
解:由题意,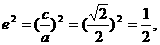
∴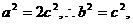 椭圆方程可设为:
椭圆方程可设为:
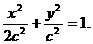 设直线l:y=k(x-1),
设直线l:y=k(x-1),
显然k≠0,将直线方程代入椭圆方程:
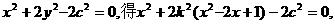
整理得: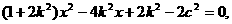 ①
①
设交点A(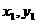 ),B(
),B( ),中点M(
),中点M(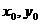 ),而中点在直线
),而中点在直线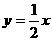 上,
上,
∴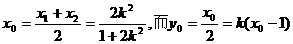 ∴
∴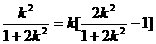 ,
,
求得:k=-1,将k=-1代入①,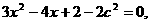 其中△>0求得
其中△>0求得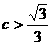 ,点
,点
F(c,0)关于直线l:y=-x+1的对称点(1,1-c)在椭圆上,代入椭圆方程:
∴1+2(1-c)2-2c2=0, ∴c=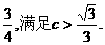
∴所求椭圆为C: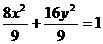 ,直线l方程为:
,直线l方程为: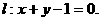
20.(本小题满分12分)
(理)设函数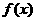 是定义在
是定义在 上的奇函数,当
上的奇函数,当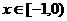 时
时 为实数).
为实数).
(I)当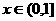 时,求
时,求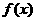 的解析式;
的解析式;
(II)若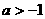 ,试判断
,试判断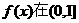 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(III)是否存在a,使得当 有最大值-6?
有最大值-6?
(理)解:(I)设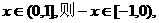
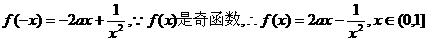 ………3分
………3分
(II)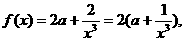
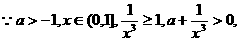
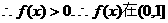 上是单调递增的.……………………………………7分
上是单调递增的.……………………………………7分
(III)当 单调递增,
单调递增,
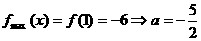 (不合题意,舍去)
(不合题意,舍去)
当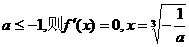 ,……………………………………………10分
,……………………………………………10分
如下表,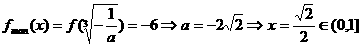 ,
,
|
x |
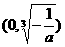 |
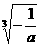 |
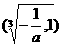 |
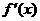 |
+ |
0 |
- |
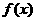 |
 |
最大值 |
 |
∴存在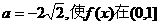 上有最大值-6
上有最大值-6
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com