
题目列表(包括答案和解析)
7.一套共7册的书计划每2年出一册,若各册书的出版年份数之和为13979,则出齐这套书的年份是
(A)1997 (B)1999 (C)2001 (D)2003
6.已知等差数列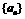 中,
中,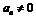 ,若
,若 ,且
,且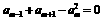 ,
, ,则
,则 等于
等于
(A)38 (B)20 (C)10 (D)9
5.设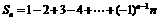 ,则
,则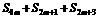 (
( N*)的值为
N*)的值为
(A)0
(B)3
(C)4 (D)随 的变化而变化
的变化而变化
4.在等差数列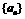 中,公差
中,公差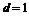 ,
,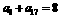 ,则
,则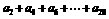 的值为
的值为
(A)40 (B)45 (C)50 (D)55
3.已知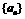 的前
的前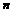 项和
项和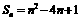 ,则
,则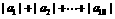 的值为
的值为
(A)67 (B)65 (C)61 (D)56
2.在等比数列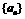 中,首项
中,首项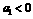 ,则
,则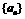 是递增数列的充要条件是公比
是递增数列的充要条件是公比
(A)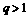 (B)
(B)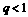 (C)
(C)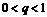 (D)
(D)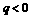
1.下列四个数中,哪一个时数列{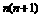 }中的一项
}中的一项
(A)380 (B)39 (C)35 (D)23
4. 应用问题
例10.用总长14.8m的钢条制作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长0.5m,那么高为多少时容器的容积最大?并求出它的最大容积。
解:设容器底面短边为xm,则另一边长为(x+0.5)m, 高为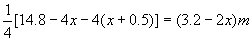 。
由3.2-2x>0且x>0,得0<x<1.6。
设容器的容积为ym3,则有y=x(x+0.5)(3.2-2x)=-2x3+2.2x2+1.6x,
(0<x<1.6)
∴ y'=-6x2+4.4x+1.6=0,
即15x2-11x-4=0,解得
。
由3.2-2x>0且x>0,得0<x<1.6。
设容器的容积为ym3,则有y=x(x+0.5)(3.2-2x)=-2x3+2.2x2+1.6x,
(0<x<1.6)
∴ y'=-6x2+4.4x+1.6=0,
即15x2-11x-4=0,解得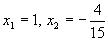 (不合题意,舍去)。
当x∈(0,1)时,y'>0;当x∈(1,1.6)时,y'<0。
∴ 函数y=-2x3+2.2x2+1.6x在(0,1)上单调递增,在[1,1.6]上单调递减。
因此,当x=1时,ymax=-2+2.2+1.6=1.8,这时,高为3.2-2×1=1.2。
故容器的高为1.2m时容器最大,最大容积为1.8m3。
例11.一艘渔艇停泊在距岸9km处,今需派人送信给距渔艇
(不合题意,舍去)。
当x∈(0,1)时,y'>0;当x∈(1,1.6)时,y'<0。
∴ 函数y=-2x3+2.2x2+1.6x在(0,1)上单调递增,在[1,1.6]上单调递减。
因此,当x=1时,ymax=-2+2.2+1.6=1.8,这时,高为3.2-2×1=1.2。
故容器的高为1.2m时容器最大,最大容积为1.8m3。
例11.一艘渔艇停泊在距岸9km处,今需派人送信给距渔艇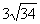 km处的海岸渔站,如果送信人步行每小时5km,船速每小时4km,问应在何处登岸再步行可以使抵达渔站的时间最省?
解析:如图示设A点为渔艇处,BC为海岸线,C为渔站,且AB=9km,
设D为海岸线上
km处的海岸渔站,如果送信人步行每小时5km,船速每小时4km,问应在何处登岸再步行可以使抵达渔站的时间最省?
解析:如图示设A点为渔艇处,BC为海岸线,C为渔站,且AB=9km,
设D为海岸线上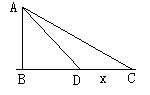 一点,CD=x,只需将时间T表示为x的函数,
∵
一点,CD=x,只需将时间T表示为x的函数,
∵ 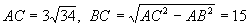 ,
由A到C的时间T,则
,
由A到C的时间T,则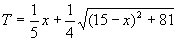 (0≤x≤15)
(0≤x≤15)
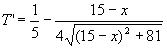 (0≤x≤15)
令T'=0,解得x=3,在x=3附近,T'由负到正,
因此在x=3处取得最小值,又
(0≤x≤15)
令T'=0,解得x=3,在x=3附近,T'由负到正,
因此在x=3处取得最小值,又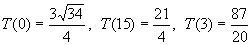 ,比较可知T(3)最小。
训练题:
1.函数y=4x2(x-2), x∈[-2,2]的最小值是_____。
2.一个外直径为10cm的球,球壳厚度为
,比较可知T(3)最小。
训练题:
1.函数y=4x2(x-2), x∈[-2,2]的最小值是_____。
2.一个外直径为10cm的球,球壳厚度为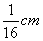 ,则球壳体积的近似值为____。
3.函数f(x)=x4-5x2+4的极大值是______,极小值是_____。
4.做一个容积为256升的方底无盖水箱,问高为多少时最省材料?
参考答案:
1. –64 2. 19.63cm3 3. 4;
,则球壳体积的近似值为____。
3.函数f(x)=x4-5x2+4的极大值是______,极小值是_____。
4.做一个容积为256升的方底无盖水箱,问高为多少时最省材料?
参考答案:
1. –64 2. 19.63cm3 3. 4;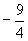 4. 设高为h,底边长为a,则所用材料为S=a2+4ah,而a2h=256,a∈(0,+∞),
∴
4. 设高为h,底边长为a,则所用材料为S=a2+4ah,而a2h=256,a∈(0,+∞),
∴ 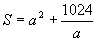 , a∈(0,+∞), 令S'(a)=
, a∈(0,+∞), 令S'(a)=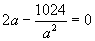 ,
∴ a=8。
显然当0<a<8时,S'(a)<0,当a>8时,S'(a)>0,因此当a=8时,S最小,此时h=4。
,
∴ a=8。
显然当0<a<8时,S'(a)<0,当a>8时,S'(a)>0,因此当a=8时,S最小,此时h=4。
13、用总长44.8m的钢条制做一个底面是等腰三角形的直三棱柱容器的框架,如果所制做容器的底面的腰长比底边长的一半长1m,那么底面的底边、腰及容器的高为多少时容器的容积最大(参考数据2.662=7.0756,3.342=11.1556)
12、设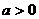 ,求函数
,求函数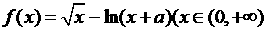 的单调区间.
的单调区间.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com