
题目列表(包括答案和解析)
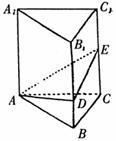
7.在底面边长为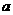 的正三棱柱ABC-A1B1C1中,D、E分别为
的正三棱柱ABC-A1B1C1中,D、E分别为
侧棱BB1、CC1上的点且EC=BC=2BD,则截面ADE与底面
ABC所成的角为 ( )
A.30° B.45°
C.60° D.75°
5.某地区高中分三类,A类校共有学生4000人,B类校共有学生2000人,C类校共有学生
3000人,现欲抽样分析某次考试的情况,若抽取900份试卷进行分析,则从A类校抽取
的试卷份数应为 ( )
A.450 B.400 C.300 D.200
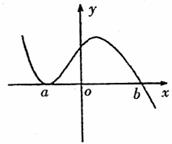 6.如图,函数
6.如图,函数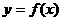 的图象如下,则函数
的图象如下,则函数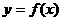 的解析式为 ( )
的解析式为 ( )
A.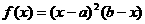
B.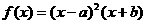
 C.
C.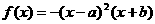
D.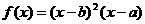
4.设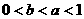 ,则下列不等式成立的是 ( )
,则下列不等式成立的是 ( )
A.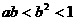 B.
B.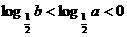
C. D.
D.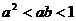
3.函数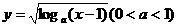 的定义域为 ( )
的定义域为 ( )
A. B.
B.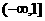 C.(1,2) D.
C.(1,2) D.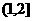
2.已知集合 等于 ( )
等于 ( )
A.1 B.2 C.1或2 D.8
且只有一项是符合题目要求的
1.若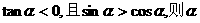 在 ( )
在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9、已知直线l过坐标原点,抛物线C的顶点在原点,焦点在x轴的正半轴上,若点A(-1,0)和点B(0,8)关于l的对称点都在C上,求直线l和抛物线C的方程。
9、已知直线l过坐标原点,抛物线C的顶点在原点,焦点在x轴的正半轴上,若点A(-1,0)和点B(0,8)关于l的对称点都在C上,求直线l和抛物线C的方程。
25.本小题考查概率的基本知识和数学期望概念及应用概率知识解决实际问题的能力,满分12分.
解:①不采取预防措施时,总费用即损失期望为400×0.3=120(万元);
②若单独采取措施甲,则预防措施费用为45万元,发生突发事件的概率为
1-0.9=0.1,损失期望值为400×0.1=40(万元),所以总费用为45+40=85(万元)
③若单独采取预防措施乙,则预防措施费用为30万元,发生突发事件的概率为1-0.85=0.15,损失期望值为400×0.15=60(万元),所以总费用为30+60=90(万元);
④若联合采取甲、乙两种预防措施,则预防措施费用为45+30=75(万元),发生突发事件的概率为(1-0.9)(1-0.85)=0.015,损失期望值为400×0.015=6(万元),所以总费用为75+6=81(万元).
综合①、②、③、④,比较其总费用可知,应选择联合采取甲、乙两种预防措施,可使总费用最少.
25.(2004.湖北理)(本小题满分12分)
某突发事件,在不采取任何预防措施的情况下发生的概率为0.3,一旦发生,将造成
400万元的损失. 现有甲、乙两种相互独立的预防措施可供采用. 单独采用甲、乙预防措施
所需的费用分别为45万元和30万元,采用相应预防措施后此突发事件不发生的概率为0.9
和0.85. 若预防方案允许甲、乙两种预防措施单独采用、联合采用或不采用,请确定预防
方案使总费用最少.
(总费用=采取预防措施的费用+发生突发事件损失的期望值.)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com