
题目列表(包括答案和解析)
2. 当x1<0,x2<0时,有-( x1+ x2)=2,即k+1=-2,k=-3…………………………(6分)
Δ=[-4(k+1)]2-16(k2+1)=32k ………………………………………………………(7分)
当k =1时,Δ>0符合题意;
当k =-3时,Δ<0舍去。
所以,满足题意的k的值为1………………………………………………………(10分)
解法二:依题意,Δ=[-4(k+1)]2-16(k2+1)=32k≥0,即k≥0………………(2分)
于是x1+ x2=k+1>0………………………………………………………………(4分)
又
∴x1>0,x2>0……………………………………………………………………(7分)
由| x1|+| x2|=2,得x1+ x2=2
k+1=2,解得k=1。
所以,满足题意的k的值为1。
1. 当x1>0,x2>0时,有x1+ x2=2,即k+1=2,k=1无解。
22、(2004年龙岩)已知关于x的方程 的两实根x1、x2满足:| x1|+| x2|=2,试求k的值.
的两实根x1、x2满足:| x1|+| x2|=2,试求k的值.
解法一:依题意, ,所以x1与x2同号……(2分)
,所以x1与x2同号……(2分)
21、(连云港市2004)关于x的一元二次方程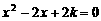 有实数根,则k的取值范围是 B
有实数根,则k的取值范围是 B
(A) (B)
(B)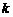 ≤
≤ (C)
(C) (D)
(D)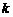 ≥
≥
20、(连云港市2004)某种商品进价为a元/件,在销售旺季,商品售价较进价高30%;销售旺季过后,商品又以7折(即原售价的70%)的价格开展促销活动,这时一件该商品的售价为D
(A) a元 (B)0.7 a元 (C)1.03 a元 (D)0.91a元
19、(陕西省2004)解方程:
解:去分母,得

18、(陕西省2004)在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是[ B ]
 A.x2+130x-1400=0
B.x2+65x-350=0
A.x2+130x-1400=0
B.x2+65x-350=0
C.x2-130x-1400=0 D.x2-65x-350=0
17、(绍兴市2004)化简:⑴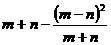 ;⑵若m,n是方程x2-3x+2=0的两个实根,求第(1)小题中代数式的值.
;⑵若m,n是方程x2-3x+2=0的两个实根,求第(1)小题中代数式的值.
(1)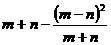 =
= .
.
(2)∵ m+n=3,m·n=2, ∴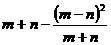 =
= =
=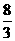 .
.
16、(绍兴市2004)已知一元二次方程 的两个根满足
的两个根满足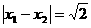 ,且a,b,c分别是△ABC的∠A,∠B,∠C的对边.若a=c,求∠B的度数.小敏解得此题的正确答案“∠B=120°”后,思考以下问题,请你帮助解答.
,且a,b,c分别是△ABC的∠A,∠B,∠C的对边.若a=c,求∠B的度数.小敏解得此题的正确答案“∠B=120°”后,思考以下问题,请你帮助解答.
(1) 若在原题中,将方程改为 ,要得到∠B=120°,而条件“a=c”不变,那么应对条件中的
,要得到∠B=120°,而条件“a=c”不变,那么应对条件中的 的值作怎样的改变?并说明理由.
的值作怎样的改变?并说明理由.
(2) 若在原题中,将方程改为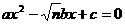 (n为正整数,n≥2),要得到∠B=120°,而条件“a=c”不变,那么条件中的
(n为正整数,n≥2),要得到∠B=120°,而条件“a=c”不变,那么条件中的 的值应改为多少(不必说明理由)?
的值应改为多少(不必说明理由)?
(1)∵ ∠B=120°,a=c, ∴ b=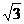 a,△=5a2>0.
a,△=5a2>0.
又∵  =
=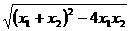 =
= . ∴
. ∴  =
= .
.
(2) =
= .
.
15、(2004年苏州)已知关于x的一元二次方程 ax2+x-a=0 ( a≠0 )
(1) 求证:对于任意非零实数a,该方程恒有两个异号的实数根;
(2) 设x1、 x2是该方程的两个根,若∣x1∣+ ∣x2∣=4,求a的值。
(1)证明:∵⊿=1+4a2, ∴⊿>0 ∴方程恒有两个实数根
设方程的两根为x1,x2, ∵a≠0, ∴x1·x2= -1<0
∴方程恒有两个异号的实数根
(2)∵x1·x2<0, ∴∣x1∣+∣x2∣=∣x1 - x2∣=4
x1+x2(x1+x2)2 - 4x1 x2=16
又∵x1+x2= -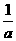 , ∴
, ∴ +4=16。∴a=±
+4=16。∴a=±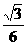
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com