
题目列表(包括答案和解析)
6.函数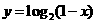 的图象是
的图象是
 A B
C
D
A B
C
D
5.对甲、乙两种种子进行发芽试验,共试验6次,每次甲、乙两种种子各选10粒,发芽数如下:
|
甲 |
6 |
5 |
8 |
4 |
9 |
6 |
|
乙 |
8 |
7 |
6 |
5 |
8 |
4 |
根据以上数据,对两种种子平均发芽数和波动性作如下判断
A.甲平均发芽数多、波动小 B.乙平均发芽数多、波动小
C.甲、乙平均发芽数一样多,甲波动小 D.甲、乙平均发芽数一样多,乙波动小
4.一个总体共有10个个体,用简单随机抽样的方法从中抽出一容量为3的样本,则某特定个体入样的概率是
A. B.
B. 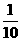
C. D.
D.
3.数列{an}的前n项和为Sn,且log3Sn=n,则{an}
A.是公比为3的等比数列 B.是公比为 的等比数列
的等比数列
C.是公差为3的等差数列 D.既不是等差数列也不是等比数列
2.设曲线y=x2+x-1在点M处切线斜率为-1,则点M的坐标为
A.(0, -1) B.(-1,-1)
C.(-1,0) D.(1,1)
1.设命题 或
或 ,命题
,命题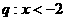 或
或 ,那么
,那么
A .若 成立则
成立则 成立
B.若
成立
B.若 成立则
成立则 成立
成立
C .若 成立则
成立则 成立
D.若
成立
D.若 成立则p成立
成立则p成立
22.(本题满分14分) 给定抛物线C:y2=4x,F是C的焦点,过点F的直线L与C相交于A、B两点。
(1)设L的斜率为1,求 与
与 夹角的大小;
夹角的大小;
(2)设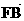 =
= ,若
,若 ∈[4,9],求L在y轴上截距的变化范围。
∈[4,9],求L在y轴上截距的变化范围。
21.(本题满分12分)若函数f(x)=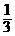 x3-
x3- ax2+(a-1)x+1在区间(1,4)内为减函数,在区间(6,+∞)上为增函数,试求实数a的取值范围。
ax2+(a-1)x+1在区间(1,4)内为减函数,在区间(6,+∞)上为增函数,试求实数a的取值范围。
20.(本题满分12分)如图,直三棱柱ABC-A1B1C1中,∠ACB=90o,AC=1,CB=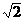 ,侧棱AA1=1,侧面AA1B1B的两条对角线交点D,B1C1的中点为M。
,侧棱AA1=1,侧面AA1B1B的两条对角线交点D,B1C1的中点为M。
(1)求证:CD⊥平面BDM;
(2)求面B1BD与面CBD所成二面角的大小。
19.(本题满分12分)已知8支球队有3支弱队,以抽签方式将这8支球队分为A、B两组,每组4支。求:
(1)A、B两组中有一组恰有两支弱队的概率;
(2)A组中至少有两支弱队的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com