
题目列表(包括答案和解析)
5.一个命题的真假与其他三个命题的真假有如下三条关系
①原命题为真,它的逆命题不一定为真
例如,原命题“若a=0,则ab=0”是真命题,它的逆命题“若ab=0,则a=0”是假命题.
②原命题为真,它的否命题不一定为真
例如,原命题“若a=0,则ab=0”是真命题,它的否命题“若a≠0,则ab≠0”是假命题.
③原命题为真,它的逆否命题一定为真
例如,原命题“若a=0,则ab=0”为真命题,它的逆否命题是“若ab≠0,则a≠0”是真命题.
4.四种命题之间的关系
互逆命题、互否命题与互为逆否命题都是说两个命题的关系,把其中一个命题叫做原命题时,另一个命
题就叫做原命题的逆命题、否命题与逆否命题.四种命题之间的关系如图所示
3.四种命题
关于逆命题,否命题与逆否命题,也可以如下表述:
①交换原命题的条件和结论,所得的命题是逆命题
如,同位角相等,两条直线平行.它的逆命题就是两条直线平行,同位角相等.
②同时否定原命题的条件和结论,所得的命题是否命题,
如上例的否命题就是同位角不相等,两条直线不平行.
③交换原命题的条件和结论,并且同时否定,所得的命题是逆否命题.
如①例的逆否命题是两条直线不平行,同位角不相等.
2.逻辑联结词:“或”、“且”、“非”这些词叫做逻辑联结词,不含逻辑联结词的命题,叫做简单命
题.由简单命题与逻辑联结词构成的命题,叫做复合命题.
①逻辑中的“或”、“且”、“非”与日常用语中的“或”、“且”、“非”的意义是不尽相同的,要结
合真值表加以理解.另外,结合集合的并集、交集、补集来理解联结词,它们的定义分别用“或”、“且”
、“非”等联结词.
②对于复合命题的理解要注意“由简单命题与…”,其中我们只注意“联结词”,而不注意“命题”.如
x>2或x<-2就不是复合命题,因为它不是命题,因此,不要认为凡是含有联结词的语句就是复合命题.
③对于三个真值表可做如下理解
ⅰ)“非p”形式复合命题的真假与p的真假相反;
ⅱ)“p且q”形式复合命题当p与q同时为真时为真,其他情况时为假;
ⅲ)“p或q”形式复合命题当p与q同时为假时为假,其他情况时为真.真值表是我们判断真假命题的直
接依据.
1.命题:初中给命题下的定义是:判断一件事情的句子,叫做命题.而高中教科书中的定义是:可以判
断真假的语句叫做命题,说法不同,实质是一样的.语句是不是命题,关键在于能不能判断其真假,也就是
判断其是否成立,不能判断真假的语句,就不能叫命题.例如:“这是一棵大树”;“x<2”都不能叫命
题,由于“大树”没有界定,就不能判断“这是一棵大树”的真假.由于x是未知数,也不能判断“x<2”是
否成立.
7.会判断充要条件
学习重点:
6.掌握充要条件,理解并学会使用推出符号“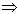 ”
”
5.反证法
4.掌握四种命题及其关系
3.会判断命题的真假,掌握真值表.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com