
题目列表(包括答案和解析)
1. 已知二次函数f(x)=(x-a)(x-b)-2(a<b),并且α、β(α<β)是方程f(x)=0的两根,则a、b、α、β的大小关系是
A.α<a<b<β B.a<α<β<b
C.a<α<b<β D.α<a<β<b
(17)(本小题满分12分)
已知10件产品中有2件是次品.
(Ⅰ)任意取出4件产品作检验,求其中恰有1件是次品的概率.
(Ⅱ)为了保证使2件次品全部检验出的概率超过0.6,至少应抽取几件产品作检验?
(18)(本小题满分12分)
已知向量 =(cos
=(cos ,sin
,sin ),
), =(cos
=(cos ,-sin
,-sin ),且x∈[
),且x∈[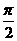 ,
, ].
].
(I)求 及
及 ;
;
(II)求函数f(x)= -
- 的最小值.
的最小值.
(19)(本小题满分12分)
三个互不相同的实数是等比数列{an}中的连续三项,又依次为某一等差数列中的第2项,第9项和第44项,这三个数的和为217.
(I) 求这三个数;
(II)记Sn为等比数列{an}的前n项和,且 <
<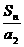 <
< ,求n的值.
,求n的值.
(20)(本小题满分12分)
在直角坐标系 中,
中, 、
、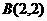 、
、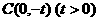 ,
,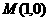 .现将坐标平面沿
.现将坐标平面沿 轴折成直二面角,记
轴折成直二面角,记 中点为
中点为 ,如图所示.
,如图所示.
(Ⅰ)求证: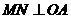 .
.
(Ⅱ)若直线 是异面直线
是异面直线 与
与 的公垂线,求
的公垂线,求 的值及直线
的值及直线 与平面
与平面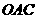 所成的角.
所成的角.

(21)(本小题满分12分)
已知 ,点
,点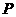 是函数
是函数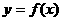 图像上的任意一点,点
图像上的任意一点,点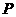 关于原点的对称点
关于原点的对称点 的轨迹是函数
的轨迹是函数 的图像当
的图像当 时,总有
时,总有 恒成立.
恒成立.
(Ⅰ)求出函数 的表达式;
的表达式;
(Ⅱ)求 的取值范围.
的取值范围.
(22)(本小题满分14分)
已知点F(1,0),直线 ,点B是l上的动点,若过B垂直于y轴的直线与线段BF的垂直平分线交于点M.
,点B是l上的动点,若过B垂直于y轴的直线与线段BF的垂直平分线交于点M.
(Ⅰ)求点M的轨迹C的方程;
(Ⅱ)设l与x轴相交于H点,直线BF与曲线C相交于P、Q两点,求证:直线HF平分∠PHQ.
(13)函数 的最小值是 .
的最小值是 .
(14)有 、
、 、
、 、
、 、
、 五名学生参加网页设计竞赛,决出了第一到第五的名次,
五名学生参加网页设计竞赛,决出了第一到第五的名次, 、
、 两位同学去问成绩,老师对
两位同学去问成绩,老师对 说:“你没能得第一名”.又对
说:“你没能得第一名”.又对 说:“你是第三名”,从这个问题分析,这五人的名次排列共有
种可能(用数字作答).
说:“你是第三名”,从这个问题分析,这五人的名次排列共有
种可能(用数字作答).
(15)设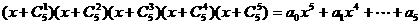 ,
,
则 .
.
(16)若对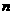 个向量
个向量 存在
存在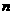 个不全为零的实数
个不全为零的实数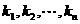 ,使得
,使得 成立,则称向量
成立,则称向量 为“线性相关”.依此规定,
能说明
为“线性相关”.依此规定,
能说明 ,
,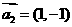 ,
, “线性相关”的实数
“线性相关”的实数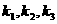 依次可以
依次可以
取 (写出一组数值即可,不必考虑所有情况).
(1)已知f(x)=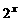 ,则f -1(
,则f -1( )=
)=
(A) (B)-1 (C)
(B)-1 (C) (D)
(D)
(2)一个单位职工150人,其中有业务人员110人,管理人员15人,后勤服务人员25人.要采用分层抽样方法从中抽取一个容量为30的样本,则应抽取管理人员
(A)15人 (B)5人 (C)3人 (D)2人
(3)已知函数 ,则集合
,则集合
 中含有元素的个数为
中含有元素的个数为
(A)0 (B)1或0 (C)1 (D)1或2
(4)从正方体的八个顶点中任取4个,其中4点恰能构成三棱锥的概率为
(A)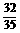 (B)
(B) (C)
(C) (D)
(D)
(5)已知x、y满足 ,则z=x+y的最大值为
,则z=x+y的最大值为
(A) 2 (B)4 (C)1 (D)
(6)直线 ,
, 互相平行的一个充分条件是
互相平行的一个充分条件是
(A)  ,
, 都平行于同一个平面
(B)
都平行于同一个平面
(B)  ,
, 与同一个平面所成的角相等
与同一个平面所成的角相等
(C)  平行于
平行于 所在的平面
(D)
所在的平面
(D)  ,
, 都垂直于同一个平面
都垂直于同一个平面
(7)圆心在抛物线 (
(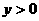 )上,并且与抛物线
)上,并且与抛物线
的准线及 轴都相切的圆的方程是
轴都相切的圆的方程是
(A)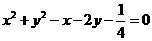 (B)
(B)
(C) (D)
(D)
(8)地球表面上从A地(北纬45°,东经120°)到B地(北纬45°,东经30°)的最短距离为(地球半径为R)
(A)R (B)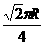 (C)
(C) (D)
(D)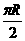
(9)若椭圆经过原点,且焦点为 ,则其离心率为
,则其离心率为
(A)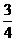 (B)
(B)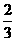 (C)
(C)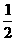 (D)
(D)
(10)曲线y=2x-x3在横坐标为-1的点处的切线为l,则点(3,2)到l的距离等于
(A) (B)
(B) (C)
(C)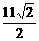 (D)
(D)
(11)已知函数 满足对任意的实数
满足对任意的实数 有
有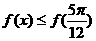 ,则当函数
,则当函数 取最小值时
取最小值时 的集合是
的集合是
(A) (B)
(B)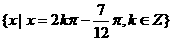
(C) (D)
(D)
(12)已知定义在R上的函数 对于任意的
对于任意的 ,都有
,都有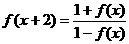 ,设
,设 ,问数列{
,问数列{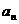 }中,值不同的项至多有
}中,值不同的项至多有
(A)12项 (B)8 项 (C)6 项 (D)4项
第Ⅱ卷(非选择题共90分)
24.(本小题满分14分)
数列{an}、{bn}分别是无穷等差、等比数列,数列{an}的前n项和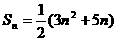 ,数列{bn}中, b3=4, b6=32.
,数列{bn}中, b3=4, b6=32.
(1) 求数列{an}和{bn}的通项公式;
(2)求数列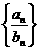 的所有项之和;
的所有项之和;
(3)记{cn}(n )是数列{an}和{bn}的所有相同项(排列顺序不变)组成的数列,求{cn}的
)是数列{an}和{bn}的所有相同项(排列顺序不变)组成的数列,求{cn}的
通项公式.
23.(本小题满分12分)
已知二次函数f (x)=ax2+bx (a, b为常数,且a≠0)满足条件:f (-x+5)=f (x-3),且方程
f (x)=x有等根.
(1) 求f (x)的解析式;
(2) 是否存在m、n(m<n),使f (x)的定义域和值域分别为[m, n]和[3m,3n]?如果存在,求出
m、n的值;如不存在,说明理由.
22.(本小题满分10分)
某俱乐部准备承办一场足球赛,预计共卖出门票2.4万张,票价有3元、5元、8元三种,
且票价3元和5元的张数之积为0.6万.设x是门票的总收入,经预算,扣除各项支出后,该俱乐部的纯收入函数为y=lg2x.试问三种门票分别为多少张时,纯收入最高?
21.(本题满分12分)
若f (x)是定义在(0, )上的增函数,且对一切x>0,满足f
)上的增函数,且对一切x>0,满足f 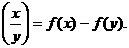
(1)求f (x)的值; (2) 若f
(6)=1,解不等式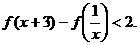
20. (本小题满分10分)
已知f (x)=2cos2x+ sin2x+a (a
sin2x+a (a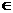 R为常数) .
R为常数) .
(1)
若x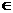 R,求f (x)的单调递增区间;
R,求f (x)的单调递增区间;
(2)
若 时, f (x)的最大值为4,求a的值.
时, f (x)的最大值为4,求a的值.
19.(本小题满分8分)
已知关于x的方程 ,其中a、b为实数.
,其中a、b为实数.
(1)
若x=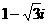 (i为虚数单位)是该方程的根,求a、b的值;
(i为虚数单位)是该方程的根,求a、b的值;
(2)
当 时, 证明该方程没有实数根.
时, 证明该方程没有实数根.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com