
题目列表(包括答案和解析)
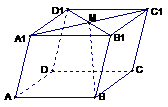
2. 如图:在平行六面体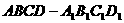 中,
中, 为
为 与
与 的交点。若
的交点。若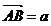 ,
,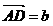 ,
,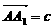 ,则下列向量中与
,则下列向量中与 相等的向量是( )
相等的向量是( )
 (A)
(A)  (B)
(B) 
(C) 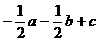 (D)
(D) 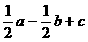
1. 函数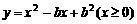 存在反函数的充要条件是( )
存在反函数的充要条件是( )
(A) 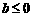 (B)
(B)
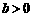 (C)
(C)
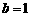 (D)
(D) 
22.(14分)设直线 与椭圆
与椭圆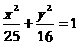 相交于A、B两点,
相交于A、B两点, 又与双曲线x2–y2=1相交于C、D两点, C、D三等分线段AB. 求直线
又与双曲线x2–y2=1相交于C、D两点, C、D三等分线段AB. 求直线 的方程.
的方程.
21. (12分)设函数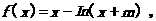 其中常数m为整数.
其中常数m为整数.
(1) 当m为何值时,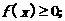
(2) 定理: 若函数g(x) 在[a, b ]上连续,且g(a) 与g(b)异号,则至少存在一点x0∈(a,b),使g(x0)=0.
试用上述定理证明:当整数m>1时,方程f(x)= 0,在[e-m-m ,e2m-m ]内有两个实根.
19. (12分)设函数
(1) 证明: 当0< a < b ,且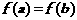 时,ab >1;
时,ab >1;
(2) 点P (x0,
y0 ) (0< x0 <1 )在曲线 上,求曲线在点P处的切线与x轴和y轴的正向所围成的三角形面积表达式(用x0表达).
上,求曲线在点P处的切线与x轴和y轴的正向所围成的三角形面积表达式(用x0表达).
20 (12分)某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到了一声巨响,正东观测点听到的时间比其他两观测点晚4s. 已知各观测点到该中心的距离都是1020m. 试确定该巨响发生的位置.(假定当时声音传播的速度为340m/ s :相关各点均在同一平面上)
18.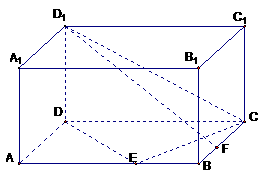 如右下图,在长方体ABCD-A1B1C1D1中,已知AB= 4, AD =3, AA1= 2. E、F分别是线段AB、BC上的点,且EB= FB=1.
如右下图,在长方体ABCD-A1B1C1D1中,已知AB= 4, AD =3, AA1= 2. E、F分别是线段AB、BC上的点,且EB= FB=1.
(1) 求二面角C-DE-C1的正切值;
(2) 求直线EC1与FD1所成的余弦值.
17. (12分)已知 成公比为2的等比数列(
成公比为2的等比数列(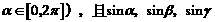 也成等比数列. 求
也成等比数列. 求 的值.
的值.
16. 函数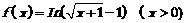 的反函数
的反函数
51. 由图(1)有面积关系: 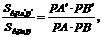 则由(2) 有体积关系:
则由(2) 有体积关系:
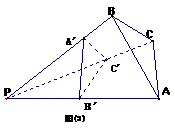
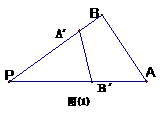
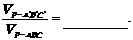
14. 已知复数z与 (z +2)2-8i 均是纯虚数,则 z = .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com